题目内容
7.下列表格是二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )| x | -2.14 | -2.13 | -2.12 | -2.11 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -2.14<x<2.13 | B. | -2.13<x<-2.12 | C. | -2.12<x<-2.11 | D. | -2.11<x<-2.10 |
分析 根据表格可知:当x=-2.13时,y=-0.01;当x=-2.12时,y=0.02,由此即可得出方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是-2.13<x<-2.12,此题得解.
解答 解:观察表格可知:当x=-2.13时,y=-0.01;当x=-2.12时,y=0.02,
∴方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是-2.13<x<-2.12.
故选B.
点评 本题考查了图象法求一元二次方程的近似根,结合表格中的数据找出方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是-2.13<x<-2.12是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
17.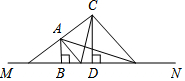 如图,AB⊥MN,CD⊥MN,垂足分别为B、D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=3或2或$\frac{3+\sqrt{41}}{2}$.
如图,AB⊥MN,CD⊥MN,垂足分别为B、D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=3或2或$\frac{3+\sqrt{41}}{2}$.
 如图,AB⊥MN,CD⊥MN,垂足分别为B、D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=3或2或$\frac{3+\sqrt{41}}{2}$.
如图,AB⊥MN,CD⊥MN,垂足分别为B、D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=3或2或$\frac{3+\sqrt{41}}{2}$.
17.关于x的方程x2+2kx-1=0的根的情况描述正确的是( )
| A. | k 为任何实数,方程都没有实数根 | |
| B. | k 为任何实数,方程都有两个不相等的实数根 | |
| C. | k 为任何实数,方程都有两个相等的实数根 | |
| D. | 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根 |
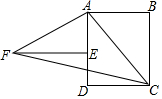 如图,四边形ABCD为长方形,△ABC旋转后能与△AEF重合,旋转中心是点A;旋转了多少度90°;连结FC,则△AFC是等腰直角三角形.
如图,四边形ABCD为长方形,△ABC旋转后能与△AEF重合,旋转中心是点A;旋转了多少度90°;连结FC,则△AFC是等腰直角三角形.