题目内容
17.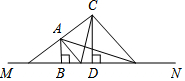 如图,AB⊥MN,CD⊥MN,垂足分别为B、D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=3或2或$\frac{3+\sqrt{41}}{2}$.
如图,AB⊥MN,CD⊥MN,垂足分别为B、D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=3或2或$\frac{3+\sqrt{41}}{2}$.
分析 分三种情形①延长CA交MN于P1,此时△P1AB∽△P1CD.②当点P2在BD上时.③当点P3在BD的延长线时.分别列出方程即可即可.
解答 解:如图,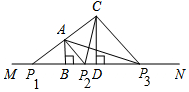
①延长CA交MN于P1,
∵AB⊥MN,CD⊥MN,
∴AB∥CD
∴△P1AB∽△P1CD,
∴$\frac{{P}_{1}B}{{P}_{1}D}$=$\frac{AB}{CD}$=2,
∴P1B=BD=3.
②当点P2在BD上时,设P2B=x,若△ABP2∽△CDP2则有$\frac{AB}{CD}$=$\frac{B{P}_{2}}{D{P}_{2}}$,
∴$\frac{2}{4}$=$\frac{x}{3-x}$,
∴x=1,
∴P2B=2,
若△ABP2∽△P2DC,则有$\frac{x}{4}$=$\frac{2}{3-x}$,方程无解.
③当点P3在BD的延长线时,∵△P3AB∽△CP3D,
∴$\frac{{P}_{3}B}{CD}$=$\frac{AB}{{P}_{3}D}$,
∴$\frac{x}{4}$=$\frac{2}{x-3}$,
∴x=$\frac{3+\sqrt{41}}{2}$或$\frac{3-\sqrt{41}}{2}$(舍弃)
∴P3B=$\frac{3+\sqrt{41}}{2}$,
综上所述,满足条件的PB的长为3或2或$\frac{3+\sqrt{41}}{2}$.
点评 本题考查相似三角形的判定和性质、一元一次方程、一元二次方程等知识,解题的关键是学会用分类讨论的思想思考问题,把问题转化为方程解决,属于中考常考题型.

练习册系列答案
相关题目
7.下列表格是二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | -2.14 | -2.13 | -2.12 | -2.11 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -2.14<x<2.13 | B. | -2.13<x<-2.12 | C. | -2.12<x<-2.11 | D. | -2.11<x<-2.10 |
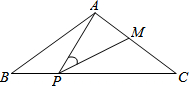 如图,在△ABC中,AB=AC=5cm,BC+8,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
如图,在△ABC中,AB=AC=5cm,BC+8,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;