题目内容
19.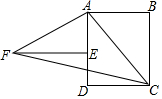 如图,四边形ABCD为长方形,△ABC旋转后能与△AEF重合,旋转中心是点A;旋转了多少度90°;连结FC,则△AFC是等腰直角三角形.
如图,四边形ABCD为长方形,△ABC旋转后能与△AEF重合,旋转中心是点A;旋转了多少度90°;连结FC,则△AFC是等腰直角三角形.
分析 由△ABC旋转后能与△AEF重合,而∠BAD=90°,所以旋转中心是点A,旋转角为90°,并且AF=AC,且∠FAC=∠BAC=90°,因此可判断△AFC的形状.
解答 解:∵△ABC旋转后能与△AEF重合.
而四边形ABCD是长方形,
∴∠BAD=90°,
∴旋转中心是点A,旋转角为90°,
∴AF=AC,且∠FAC=∠BAD=90°,
∴△AFC是等腰直角三角形.
故答案为:A,90°,等腰直角.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了长方形和等腰直角三角形的性质.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
10.已知等腰三角形的两边为2和4,则它的周长为( )
| A. | 8 | B. | 6 | C. | 8或10 | D. | 10 |
7.下列表格是二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | -2.14 | -2.13 | -2.12 | -2.11 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -2.14<x<2.13 | B. | -2.13<x<-2.12 | C. | -2.12<x<-2.11 | D. | -2.11<x<-2.10 |

 如图所示,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点A处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点B处有食物,蚂蚁要吃到食物所走的最短路线长度是17cm.
如图所示,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点A处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点B处有食物,蚂蚁要吃到食物所走的最短路线长度是17cm.