题目内容
17.关于x的方程x2+2kx-1=0的根的情况描述正确的是( )| A. | k 为任何实数,方程都没有实数根 | |
| B. | k 为任何实数,方程都有两个不相等的实数根 | |
| C. | k 为任何实数,方程都有两个相等的实数根 | |
| D. | 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根 |
分析 根据方程的系数结合根的判别式即可得出△=4k2+4>0,由此即可得出k可以为任何实数且原方程总有两个不相等的实数根,此题得解.
解答 解:∵在方程x2+2kx-1=0中,△=(2k)2-4×1×(-1)=4k2+4>0,
∴k为任何实数且方程x2+2kx-1=0有两个不相等的实数根.
故选B.
点评 本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的两个实数根”是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列表格是二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
| x | -2.14 | -2.13 | -2.12 | -2.11 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | -2.14<x<2.13 | B. | -2.13<x<-2.12 | C. | -2.12<x<-2.11 | D. | -2.11<x<-2.10 |
7.“十•一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客a+2.4万人
(2)请判断七天内游客人数最多的是3日;最少的是7日.它们相差2.2万人?
(3)若9月30日的游客人数0.5万人,该景区在10月7号接待了多少游客?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是3日;最少的是7日.它们相差2.2万人?
(3)若9月30日的游客人数0.5万人,该景区在10月7号接待了多少游客?
 如图所示,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点A处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点B处有食物,蚂蚁要吃到食物所走的最短路线长度是17cm.
如图所示,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点A处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点B处有食物,蚂蚁要吃到食物所走的最短路线长度是17cm.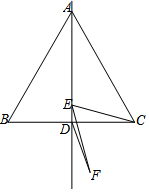 如图,已知等边△ABC边长为8 cm,D为BC中点,E为直线AD上一动点,将EC绕着点E顺时针旋转60°得到线段EF,连接DF,则线段DF最小值为2.
如图,已知等边△ABC边长为8 cm,D为BC中点,E为直线AD上一动点,将EC绕着点E顺时针旋转60°得到线段EF,连接DF,则线段DF最小值为2.