题目内容
我们把能够平分一个图形面积的直线叫“好线”,如图1.

问题情境:如图2,M是圆O内的一定点,请在图2中作出两条“好线”(要求其中一条“好线”必须过点M),使它们将圆O的面积四等分.
小明的思路是:如图3,过点M、O画一条“好线”,过O作OM的垂线,即为另一条“好线”.所以这两条“好线”将的圆O的面积四等分.
问题迁移:
(1)请在图4中作出两条“好线”,使它们将?ABCD的面积四等分;
(2)如图5,M是正方形ABCD内一定点,请在图5中作出两条“好线”(要求其中一条“好线”必须过点M),使它们将正方形ABCD的面积四等分;
(3)如图6,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,点Q是边BC一点,请作出“好线”PQ将四边形ABCD的面积分成相等的两部分.

问题情境:如图2,M是圆O内的一定点,请在图2中作出两条“好线”(要求其中一条“好线”必须过点M),使它们将圆O的面积四等分.
小明的思路是:如图3,过点M、O画一条“好线”,过O作OM的垂线,即为另一条“好线”.所以这两条“好线”将的圆O的面积四等分.
问题迁移:
(1)请在图4中作出两条“好线”,使它们将?ABCD的面积四等分;
(2)如图5,M是正方形ABCD内一定点,请在图5中作出两条“好线”(要求其中一条“好线”必须过点M),使它们将正方形ABCD的面积四等分;
(3)如图6,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,点Q是边BC一点,请作出“好线”PQ将四边形ABCD的面积分成相等的两部分.
考点:四边形综合题,三角形的面积
专题:
分析:(1)由四边形ABCD是平行四边形,直线AC,BD是角平分线所在的直线,可得AO=CO,BO=DO,所以S△AOB=S△BOC=S△OCD=S△AOD,即可得出AC,BD将?ABCD的面积四等分,
(2)连接AC、BD相交于点O,作直线OM分别交AD、BC于P、Q两点,过点O作用OM的垂线分别交AB、CD于E、F两点,则直线OM、EF将正方形ABCD的面积四等分.
(3)当BQ=CD=时,PQ将四边形ABCD面积二等分.
(2)连接AC、BD相交于点O,作直线OM分别交AD、BC于P、Q两点,过点O作用OM的垂线分别交AB、CD于E、F两点,则直线OM、EF将正方形ABCD的面积四等分.
(3)当BQ=CD=时,PQ将四边形ABCD面积二等分.
解答:解:(1)如图4,直线AC,BD将?ABCD的面积四等分,
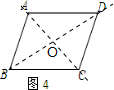
理由如下:
∵四边形ABCD是平行四边形,直线AC,BD是角平分线所在的直线,
∴AO=CO,BO=DO,
∴S△AOB=S△BOC=S△OCD=S△AOD,
∴AC,BD将?ABCD的面积四等分,
(2)如图5,连接AC、BD相交于点O,作直线OM分别交AD、BC于P、Q两点,过点O作用OM的垂线分别交AB、CD于E、F两点,则直线OM、EF将正方形ABCD的面积四等分.
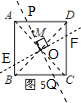
理由如下:
∵点O是正方形ABCD对角线的交点,
∴点O是正方形ABCD的对称中心.
∴AP=CQ,EB=DF.
在△AOP和△EOB中,
∵∠AOP=90°-∠AOE,∠BOE=90°-∠AOE,
∴∠AOP=∠BOE.
∵OA=OB,∠OAP=∠EBO=45°,
∴△AOP≌△EOB(ASA).
∴AP=BE=DF=CQ.
∴AE=BQ=CF=PD.
设点O到正方形ABCD一边的距离为d,.
∴
(AP+AE)d=
(BE+BQ)d=
(CQ+CF)d=
(DF+PD)d.
∴S四边形APOE=S四边形BEOQ=F四边形CQOF=S四边形DFOP.
∴直线EF、PQ将正方形ABCD面积四等分.
(3)存在.当BQ=CD=时,PQ将四边形ABCD面积二等分.
理由如下:
如图6,延长BA至点E,使AE=CD,延长CD至点F,使DF=AB,连接EF.
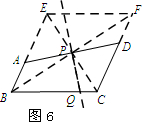
∵BE∥CF,BE=CF.
∴四边形BCFE为平行四边形.
∵BC=BE=AB+CD,
∴平行四边形CBFE为菱形.
连接BF交AD于点M,则△MAB≌△MDF.
∴AM=DM,即点P、M重合.
∴点P是菱形EBCF对角线的交点.
在BC上截取BQ=CD,则CQ=AB.
设点P到菱形EBCF一边的距离为d,
∴S△ABP+S△QBP=
(AB+BQ)d=
(CQ+CD)d=S△CQP+S△CDP.
∴当BQ=CD时,直线PQ将四边形ABCD的面积分成相等的两部分.

理由如下:
∵四边形ABCD是平行四边形,直线AC,BD是角平分线所在的直线,
∴AO=CO,BO=DO,
∴S△AOB=S△BOC=S△OCD=S△AOD,
∴AC,BD将?ABCD的面积四等分,
(2)如图5,连接AC、BD相交于点O,作直线OM分别交AD、BC于P、Q两点,过点O作用OM的垂线分别交AB、CD于E、F两点,则直线OM、EF将正方形ABCD的面积四等分.

理由如下:
∵点O是正方形ABCD对角线的交点,
∴点O是正方形ABCD的对称中心.
∴AP=CQ,EB=DF.
在△AOP和△EOB中,
∵∠AOP=90°-∠AOE,∠BOE=90°-∠AOE,
∴∠AOP=∠BOE.
∵OA=OB,∠OAP=∠EBO=45°,
∴△AOP≌△EOB(ASA).
∴AP=BE=DF=CQ.
∴AE=BQ=CF=PD.
设点O到正方形ABCD一边的距离为d,.
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形APOE=S四边形BEOQ=F四边形CQOF=S四边形DFOP.
∴直线EF、PQ将正方形ABCD面积四等分.
(3)存在.当BQ=CD=时,PQ将四边形ABCD面积二等分.
理由如下:
如图6,延长BA至点E,使AE=CD,延长CD至点F,使DF=AB,连接EF.

∵BE∥CF,BE=CF.
∴四边形BCFE为平行四边形.
∵BC=BE=AB+CD,
∴平行四边形CBFE为菱形.
连接BF交AD于点M,则△MAB≌△MDF.
∴AM=DM,即点P、M重合.
∴点P是菱形EBCF对角线的交点.
在BC上截取BQ=CD,则CQ=AB.
设点P到菱形EBCF一边的距离为d,
∴S△ABP+S△QBP=
| 1 |
| 2 |
| 1 |
| 2 |
∴当BQ=CD时,直线PQ将四边形ABCD的面积分成相等的两部分.
点评:本题主要考查了四边形综综合题及三角形的面积,解题的关键是熟记等底等高的三角形面积相等.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
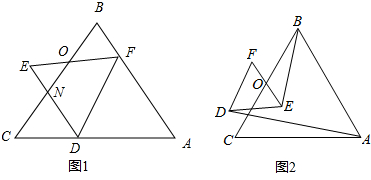
 如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.
如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.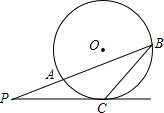 如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.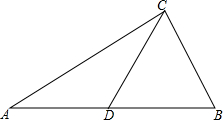 已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.
已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.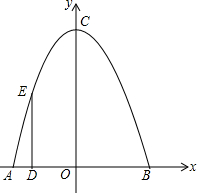 《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?
《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?