题目内容
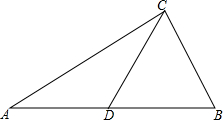 已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.
已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.考点:勾股定理的逆定理,全等三角形的判定与性质
专题:证明题
分析:作AE平行于BC交CD的延长线于E,首先证明△AED≌△BCD,可得AE=BC=5,ED=CD,再利用勾股定理逆定理可证明△AEC是直角三角形,进而可得∠CAB+∠EAB=90°,再由∠B=∠EAB,可得∠CAB+∠B=90°,从而证明△ABC是直角三角形.
解答:证明: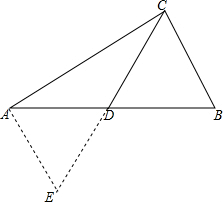 作AE平行于BC交CD的延长线于E,
作AE平行于BC交CD的延长线于E,
∵D是AB中点,
∴AD=BD,
∵AE∥CB,
∴∠B=∠EAB,
在△ADE和△BDC中,
,
∴△AED≌△BCD(ASA),
∴AE=BC=5,ED=CD,
∴EC=13,
∵AC=12,
∵52+122=132,
∴△AEC是直角三角形.
∴∠CAE=90°,
∴∠CAB+∠EAB=90°,
∵∠B=∠EAB,
∴∠CAB+∠B=90°,
∴△ABC是直角三角形.
 作AE平行于BC交CD的延长线于E,
作AE平行于BC交CD的延长线于E,∵D是AB中点,
∴AD=BD,
∵AE∥CB,
∴∠B=∠EAB,
在△ADE和△BDC中,
|
∴△AED≌△BCD(ASA),
∴AE=BC=5,ED=CD,
∴EC=13,
∵AC=12,
∵52+122=132,
∴△AEC是直角三角形.
∴∠CAE=90°,
∴∠CAB+∠EAB=90°,
∵∠B=∠EAB,
∴∠CAB+∠B=90°,
∴△ABC是直角三角形.
点评:此题主要考查了勾股定理逆定理,关键是正确画出辅助线,证明△AEC是直角三角形.

练习册系列答案
相关题目
 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.
如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度. 已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
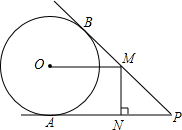 如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.