题目内容
 如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.
如图,⊙O是正五边形ABCDE的外接圆,对角线AC、BD相交于点P.(1)求∠APB的度数;
(2)求证:AC=AB+BP.
考点:正多边形和圆
专题:
分析:(1)运用圆周角定理,直接求出∠ABP=72°,即可解决问题.
(2)证明AB=AP;证明PB=PC,即可解决问题.
(2)证明AB=AP;证明PB=PC,即可解决问题.
解答: 解:(1)如图,∵⊙O是正五边形ABCDE的外接圆,
解:(1)如图,∵⊙O是正五边形ABCDE的外接圆,
∴∠ABP=
×
×360°=72°.
(2)∵⊙O是正五边形ABCDE的外接圆,
∴∠BAC=
×
×360°=36°,
∴∠APB=180°-72°-36°=72°,
∴∠ABP=∠APB,
∴AB=AP;
同理可证:∠PBC=∠PCB=36°,
∴PB=PC,
∴AC=AB+BP.
 解:(1)如图,∵⊙O是正五边形ABCDE的外接圆,
解:(1)如图,∵⊙O是正五边形ABCDE的外接圆,∴∠ABP=
| 1 |
| 2 |
| 2 |
| 5 |
(2)∵⊙O是正五边形ABCDE的外接圆,
∴∠BAC=
| 1 |
| 2 |
| 1 |
| 5 |
∴∠APB=180°-72°-36°=72°,
∴∠ABP=∠APB,
∴AB=AP;
同理可证:∠PBC=∠PCB=36°,
∴PB=PC,
∴AC=AB+BP.
点评:该题主要考查了正多边形和圆的关系及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
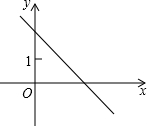 如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )
如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )| A、3 | B、2 | C、1或2 | D、2或3 |
 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.
如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.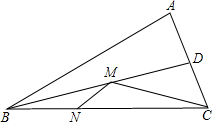 在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少?
在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少? 已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
已知⊙O1与⊙O2相交于A、B,点O1在⊙O2上,AC是⊙O1的直径,直线CB与⊙O2相交于点D,连AD.
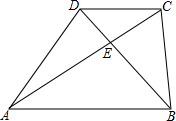 四边形ABCD中,AB∥CD,AC、BD交于点E,已知S△DCE:S△ADE=4:6.
四边形ABCD中,AB∥CD,AC、BD交于点E,已知S△DCE:S△ADE=4:6.