题目内容
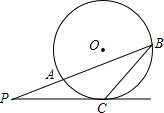 如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.考点:切线的判定
专题:证明题
分析:连接OA,OC,AC,根据PC2=PA•PB和∠P=∠P,可证明△PCA∽△PBC,则∠PCA=∠PBC,再由已知条件即可得出PC⊥OC,则PC是⊙O的切线.
解答: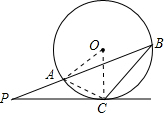 证明:连接OA,OC,AC,
证明:连接OA,OC,AC,
∵PC2=PA•PB,∠P=∠P,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
设∠PCA=∠PBC=x°,
∴∠AOC=2x°,
∵OA=OC,
∴∠OAC=OCA=
=90°-x°,
∴∠PCO=∠PCA+∠OCA=90°-x°+x°=90°,
∴PC⊥OC,
∴PC是⊙O的切线.
 证明:连接OA,OC,AC,
证明:连接OA,OC,AC,∵PC2=PA•PB,∠P=∠P,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
设∠PCA=∠PBC=x°,
∴∠AOC=2x°,
∵OA=OC,
∴∠OAC=OCA=
| 180°-2x° |
| 2 |
∴∠PCO=∠PCA+∠OCA=90°-x°+x°=90°,
∴PC⊥OC,
∴PC是⊙O的切线.
点评:本题考查了切线的判定,以及三角形的内角和定理、相似三角形的判定,是一道综合性的题目,是中考压轴题,难度中等.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 有理数m、n在数轴上的位置如图所示,则下列不等式关系正确的是( )
有理数m、n在数轴上的位置如图所示,则下列不等式关系正确的是( )| A、m<n |
| B、m>-n |
| C、|m|<|n| |
| D、m2>n2 |
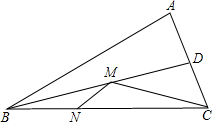 在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少?
在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少? 正六边形的边长为8,则阴影部分的面积是多少?
正六边形的边长为8,则阴影部分的面积是多少?
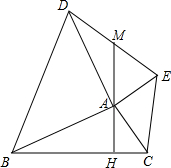 如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.
如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.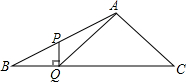 在△ABC中,∠B=30°,P为AB上的一点,
在△ABC中,∠B=30°,P为AB上的一点,