题目内容
△ABC和△DEF均为等边三角形
(1)如图1,点D、F分别在AC、AB上,请找一个与△ADF相似的三角形:△ADF∽ ;
(2)如图2,O为BC、EF的中点,则AD:BE的值是多少?
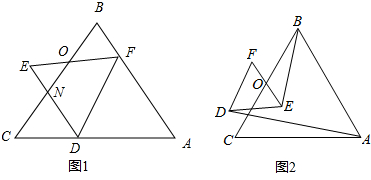
(1)如图1,点D、F分别在AC、AB上,请找一个与△ADF相似的三角形:△ADF∽
(2)如图2,O为BC、EF的中点,则AD:BE的值是多少?

考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易得∠DFE=60°,∠A=∠B=60°,即可求得∠BFO=∠ADF,即可证明△ADF∽△BFO;
(2)连接OD,OA,易证∠DOE=∠AOB=90°,OD=
EO,AO=
BO,即可求得∠BOE=∠AOD,即可证明△BOE∽△AOD,可得
=
,即可解题.
(2)连接OD,OA,易证∠DOE=∠AOB=90°,OD=
| 3 |
| 3 |
| AD |
| BE |
| AO |
| BO |
解答:解:(1)∵△ABC和△DEF均为等边三角形,
∴∠DFE=60°,∠A=∠B=60°,
∴∠BFO+∠AFD=120°,∠AFD+∠ADF=120°,
∴∠BFO=∠ADF,
∴△ADF∽△BFO;
(2)连接OD,OA,
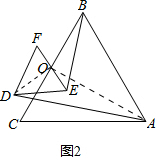
∵O为BC、EF的中点,
∴∠DOE=∠AOB=90°,OD=
EO,AO=
BO,
∵∠BOE=∠AOB+∠AOE,∠AOD=∠DOE+∠AOE,
∴∠BOE=∠AOD,
∴△BOE∽△AOD,
∴
=
=
.
∴∠DFE=60°,∠A=∠B=60°,
∴∠BFO+∠AFD=120°,∠AFD+∠ADF=120°,
∴∠BFO=∠ADF,
∴△ADF∽△BFO;
(2)连接OD,OA,

∵O为BC、EF的中点,
∴∠DOE=∠AOB=90°,OD=
| 3 |
| 3 |
∵∠BOE=∠AOB+∠AOE,∠AOD=∠DOE+∠AOE,
∴∠BOE=∠AOD,
∴△BOE∽△AOD,
∴
| AD |
| BE |
| AO |
| BO |
| 3 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证△BOE∽△AOD是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )
如图,直线l:y=-x+b,点M(3,2)关于直线l的对称点M1落在y轴上,则b的值等于( )| A、3 | B、2 | C、1或2 | D、2或3 |
 有理数m、n在数轴上的位置如图所示,则下列不等式关系正确的是( )
有理数m、n在数轴上的位置如图所示,则下列不等式关系正确的是( )| A、m<n |
| B、m>-n |
| C、|m|<|n| |
| D、m2>n2 |
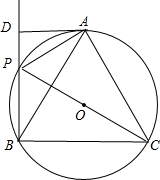
 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.
如图,一条小河的两岸有一段是平行的,在河的一岸每隔6m有一棵树,在河的对岸每隔60m有一根电线杆,在有树的一岸离岸边30m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽度.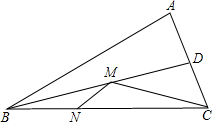 在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少?
在锐角△ABC中,BC=4,∠ABC=30°,BD平分∠ABC,点M、N分别是BD、BC上的动点,连接MN、CM,则CM+MN的最小值是多少?