题目内容
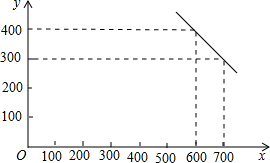 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.(1)根据图象,求一次函数y=kx+b的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,①试用销售单价x表示毛利润S;②试问销售单价定为多少时,该公司可获得最大利润?最大利润是多少?此时的销售量是多少?
考点:二次函数的应用
专题:
分析:(1)把点(700,300)和点(600,400)分别代入一次函数y=kx+b,解方程组求得k和b的值,即可得到一次函数y=kx+b的表达式.
(2)由题意可得 S=y•x-500y,化简可得S=-x2+1500x-500000,利用二次函数性质求出函数的最大值以及函数取最大值时x的值.
(2)由题意可得 S=y•x-500y,化简可得S=-x2+1500x-500000,利用二次函数性质求出函数的最大值以及函数取最大值时x的值.
解答:解:(1)把点(700,300)和点(600,400)分别代入一次函数y=kx+b可得 300=700k+b,且400=600k+b,
解得 k=-1,b=1000,故一次函数y=kx+b的表达式为 y=-x+1000.
(2)①∵公司获得的毛利润(毛利润=销售总价-成本总价)为S,则 S=y•x-500y=(-x+1000 )x-500(-x+1000)=-x2+1500x-500000.
②故函数S的对称轴为x=750,满足 500≤x≤800,故当x=750时,函数S取得最大值为62500元,
y=-750+1000=250,
即当销售单价定为750元/价时,该公司可获得最大的毛利润为62500元,销量为250件.
解得 k=-1,b=1000,故一次函数y=kx+b的表达式为 y=-x+1000.
(2)①∵公司获得的毛利润(毛利润=销售总价-成本总价)为S,则 S=y•x-500y=(-x+1000 )x-500(-x+1000)=-x2+1500x-500000.
②故函数S的对称轴为x=750,满足 500≤x≤800,故当x=750时,函数S取得最大值为62500元,
y=-750+1000=250,
即当销售单价定为750元/价时,该公司可获得最大的毛利润为62500元,销量为250件.
点评:本题主要考查用待定系数法求直线方程,二次函数性质的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
下列结论中正确的是( )
| A、数轴上任一点都表示唯一的有理数 |
| B、两个无理数乘积一定是无理数 |
| C、两个无理数之和一定是无理数 |
| D、数轴上任意两点之间还有无数个点 |
 如图,在平面直角坐标系中,直线AB由直线y=3x沿x轴向左平移3个单位长度所得,则直线AB与坐标轴所围成的三角形的面积为
如图,在平面直角坐标系中,直线AB由直线y=3x沿x轴向左平移3个单位长度所得,则直线AB与坐标轴所围成的三角形的面积为 已知长方形ABCD中,AB=6,BC=8,将纸片折叠,使得点A和点C重合,折痕为EF,如图,则EF的长为多少?
已知长方形ABCD中,AB=6,BC=8,将纸片折叠,使得点A和点C重合,折痕为EF,如图,则EF的长为多少? 如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,PQ∥AB交AC于D点,且∠ODQ=90°,求D点的坐标.
如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,PQ∥AB交AC于D点,且∠ODQ=90°,求D点的坐标.