题目内容
 已知长方形ABCD中,AB=6,BC=8,将纸片折叠,使得点A和点C重合,折痕为EF,如图,则EF的长为多少?
已知长方形ABCD中,AB=6,BC=8,将纸片折叠,使得点A和点C重合,折痕为EF,如图,则EF的长为多少?考点:翻折变换(折叠问题)
专题:几何图形问题
分析:连接AF,根据折叠的性质,得EF垂直平分AC,则AE=CE.设AE=x,则BE=8-x,根据勾股定理求得x的值,再根据勾股定理求得AC的长,即可求得AO的长,再根据勾股定理求得OE的长,进而求得EF=2OE.
解答: 解:连接AE.
解:连接AE.
∵将纸片折叠,使得点A和点C重合,
∴AE=CE.
∴BC=8,
∴设AE=x,则BE=8-x.
在Rt△ABE中,
∵AB=6,BE=8-x,
∴AE2=AB2+BE2,
即x2=36+(8-x)2,
解得x=
.
在Rt△ABC中,
∵AB=6,BC=8,
∴AC=
=
=10,则AO=5.
同理,在Rt△AOE中,OE=
=
=
,
∵EF是折痕,
∴EF=2OE=
.
 解:连接AE.
解:连接AE.∵将纸片折叠,使得点A和点C重合,
∴AE=CE.
∴BC=8,
∴设AE=x,则BE=8-x.
在Rt△ABE中,
∵AB=6,BE=8-x,
∴AE2=AB2+BE2,
即x2=36+(8-x)2,
解得x=
| 25 |
| 4 |
在Rt△ABC中,
∵AB=6,BC=8,
∴AC=
| AB2+BC2 |
| 62+82 |
同理,在Rt△AOE中,OE=
| AE2-AO2 |
(
|
| 15 |
| 4 |
∵EF是折痕,
∴EF=2OE=
| 15 |
| 2 |
点评:本题考查的是折叠的性质,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列计算正确的是( )
| A、3a-2a=1 | ||
| B、2a2+a2=3a4 | ||
| C、-2(a-b)=2b-2a | ||
D、
|
 如图:AD是△ABC的高,
如图:AD是△ABC的高,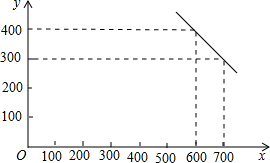 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示. 如图,双曲线
如图,双曲线