题目内容
 如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,PQ∥AB交AC于D点,且∠ODQ=90°,求D点的坐标.
如图,已知直角梯形OABC的A点在x轴上,C点在y轴上,OC=6,OA=OB=10,PQ∥AB交AC于D点,且∠ODQ=90°,求D点的坐标.考点:一次函数综合题
专题:
分析:首先求出BC的长,即可得出B点坐标,进而得出E点位置,进而求出直线DO解析式,进而得出直线AC的解析式,进而求出两函数交点坐标得出答案即可.
解答: 解:连接BO,延长OD,交AB于E,
解:连接BO,延长OD,交AB于E,
∵AB∥PQ,OD⊥PQ,
∴OD⊥AB,
又∵OA=OB,
∴点E是AB中点,
∵CB=
=8,
∴B点坐标(8,6),
又∵A(10,0),
∴AB的中点E点坐标为(9,3),
设DO的解析式为:y=ax,
∴9a=3,
解得:a=
,
∴OD的表达式为:y=
x,
∵A(10,0),C(0,6),
设AC的解析式为:y=kx+b,
,
解得:
∴AC的表达式为:y=-
x+6,
由
,
解得:
,
故点D的坐标为(
,
).
 解:连接BO,延长OD,交AB于E,
解:连接BO,延长OD,交AB于E,∵AB∥PQ,OD⊥PQ,
∴OD⊥AB,
又∵OA=OB,
∴点E是AB中点,
∵CB=
| OB2-OC2 |
∴B点坐标(8,6),
又∵A(10,0),
∴AB的中点E点坐标为(9,3),
设DO的解析式为:y=ax,
∴9a=3,
解得:a=
| 1 |
| 3 |
∴OD的表达式为:y=
| 1 |
| 3 |
∵A(10,0),C(0,6),
设AC的解析式为:y=kx+b,
|
解得:
|
∴AC的表达式为:y=-
| 3 |
| 5 |
由
|
解得:
|
故点D的坐标为(
| 45 |
| 7 |
| 15 |
| 7 |
点评:此题主要考查了一次函数的综合以及待定系数法求一次函数解析式以及函数交点求法等知识,得出E点坐标是解题关键.

练习册系列答案
相关题目
下列说法中正确的有( )
①若∠A:∠B:∠C=1:1:2,则△ABC是直角三角形;
②若∠A-∠B=∠C,则△ABC是直角三角形;
③若三角形的三边分别为9、40、41,则△ABC是直角三角形;
④若三角形的三边分别为2n、3n、4n,则△ABC是直角三角形.
①若∠A:∠B:∠C=1:1:2,则△ABC是直角三角形;
②若∠A-∠B=∠C,则△ABC是直角三角形;
③若三角形的三边分别为9、40、41,则△ABC是直角三角形;
④若三角形的三边分别为2n、3n、4n,则△ABC是直角三角形.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,P为∠AOB内一点,PC⊥OA于点C,PD⊥OB于点D,PC=PD,连结OP,可通过证明△POC≌△POD得∠AOP=∠BOP.适用的判定定理是( )
如图,P为∠AOB内一点,PC⊥OA于点C,PD⊥OB于点D,PC=PD,连结OP,可通过证明△POC≌△POD得∠AOP=∠BOP.适用的判定定理是( )| A、SAS | B、ASA |
| C、SSS | D、HL |
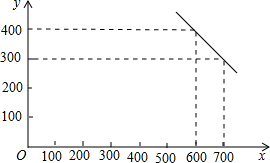 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示. 如图,双曲线
如图,双曲线