题目内容
有一块三角形的木板ABC,量得AB=13cm,BC=14cm,AC=15cm,你能求出这块木板的面积吗?
考点:勾股定理的应用
专题:几何图形问题
分析:过点A作AD⊥BC,利用勾股定理求出AD的长,再利用三角形的面积公式求出△ABC的面积即可.
解答: 解:设CD=xcm,则BD=(14-x)cm,
解:设CD=xcm,则BD=(14-x)cm,
在Rt△ACD中,AD2+x2=152,
在Rt△ADB中,AD2=132-(14-x)2,
∴152-x2=132-(14-x)2,
解得:x=9,
∴BD=5(cm),
在Rt△ACD中,AD=
=12(cm),
∴△ABC的面积=
×BC•AD=
×14×12=84(cm2).
 解:设CD=xcm,则BD=(14-x)cm,
解:设CD=xcm,则BD=(14-x)cm,在Rt△ACD中,AD2+x2=152,
在Rt△ADB中,AD2=132-(14-x)2,
∴152-x2=132-(14-x)2,
解得:x=9,
∴BD=5(cm),
在Rt△ACD中,AD=
| 132-52 |
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了勾股定理应用,解决本题的关键在于利用两个直角三角形的公共边找到突破点.主要利用了勾股定理进行解答.

练习册系列答案
相关题目
下列说法中正确的有( )
①若∠A:∠B:∠C=1:1:2,则△ABC是直角三角形;
②若∠A-∠B=∠C,则△ABC是直角三角形;
③若三角形的三边分别为9、40、41,则△ABC是直角三角形;
④若三角形的三边分别为2n、3n、4n,则△ABC是直角三角形.
①若∠A:∠B:∠C=1:1:2,则△ABC是直角三角形;
②若∠A-∠B=∠C,则△ABC是直角三角形;
③若三角形的三边分别为9、40、41,则△ABC是直角三角形;
④若三角形的三边分别为2n、3n、4n,则△ABC是直角三角形.
| A、1个 | B、2个 | C、3个 | D、4个 |
不等式组
的解是( )
|
| A、-6<x≤1 |
| B、-6<x<1 |
| C、-6≤x<1 |
| D、-6≤x≤1 |
 如图,长方形ABCD正好被分成6个正方形.如果中间最小的正方形面积等于1,那么长方形ABCD的面积等于
如图,长方形ABCD正好被分成6个正方形.如果中间最小的正方形面积等于1,那么长方形ABCD的面积等于 如图:AD是△ABC的高,
如图:AD是△ABC的高, 已知:(如图)在Rt△ABC中,∠C=90°,D、E分别为BC、AC的中点,AD=5,
已知:(如图)在Rt△ABC中,∠C=90°,D、E分别为BC、AC的中点,AD=5,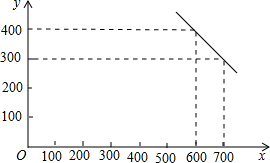 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量(件)与销售单价x(元/件)可近似看做-次函数y=kx+b的关系,如图所示.