题目内容
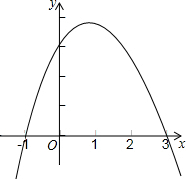 二次函数y=ax2+bx+c(a、b、c是常数a≠0)的大致图象如图所示,抛物线交x轴于点(-1,0),(3,0).则下列说法中,正确的是( )
二次函数y=ax2+bx+c(a、b、c是常数a≠0)的大致图象如图所示,抛物线交x轴于点(-1,0),(3,0).则下列说法中,正确的是( )| A、abc>0 |
| B、b-2a=0 |
| C、3a+c>0 |
| D、9a+6b+4c>0 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答: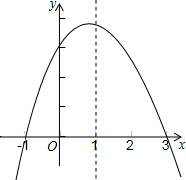 解:A、∵根据图示知,抛物线开口方向向下,∴a<0;
解:A、∵根据图示知,抛物线开口方向向下,∴a<0;
∵抛物线交x轴于点(-1,0),(3,0),
∴对称轴x=
=-
=1,
∴b=-2a>0.
∵根据图示知,抛物线与y轴交于正半轴,
∴c>0,
∴abc<0.
故本选项错误;
B、∵对称轴x=
=-
=1,
∴b=-2a,
∴b+2a=0.
故本选项错误;
C、根据图示知,当x=-1时,y=0,即a-b+c=a+2a+c=3a+c=0.
故本选项错误;
D、∵a<0,c>0,
∴-3a>0,4c>0,
∴-3a+4c>0,
∴9a+6b+4c=9a-12a+4c=-3a+4c>0,即9a+6b+4c>0.
故本选项正确.
故选D.
 解:A、∵根据图示知,抛物线开口方向向下,∴a<0;
解:A、∵根据图示知,抛物线开口方向向下,∴a<0;∵抛物线交x轴于点(-1,0),(3,0),
∴对称轴x=
| -1+3 |
| 2 |
| b |
| 2a |
∴b=-2a>0.
∵根据图示知,抛物线与y轴交于正半轴,
∴c>0,
∴abc<0.
故本选项错误;
B、∵对称轴x=
| -1+3 |
| 2 |
| b |
| 2a |
∴b=-2a,
∴b+2a=0.
故本选项错误;
C、根据图示知,当x=-1时,y=0,即a-b+c=a+2a+c=3a+c=0.
故本选项错误;
D、∵a<0,c>0,
∴-3a>0,4c>0,
∴-3a+4c>0,
∴9a+6b+4c=9a-12a+4c=-3a+4c>0,即9a+6b+4c>0.
故本选项正确.
故选D.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
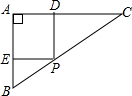 如图,Rt△ABC中,∠BAC=90°,AB=3,AC=4,P是BC上一点,作PE⊥AB于E,PD⊥AC于D.设BP=x,则PD+PE等于( )
如图,Rt△ABC中,∠BAC=90°,AB=3,AC=4,P是BC上一点,作PE⊥AB于E,PD⊥AC于D.设BP=x,则PD+PE等于( )A、4-
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
| B、3π | ||
C、
| ||
| D、6π |
 下列图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )
下列图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )| A、36 | B、55 | C、70 | D、91 |
 如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则AB的长为( )
如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则AB的长为( )| A、4 | B、6 | C、8 | D、10 |
 如图,四边形ABCD是平行四边形,AC是对角线,BE⊥AC,垂足为E;DF⊥AC,垂足为F.
如图,四边形ABCD是平行四边形,AC是对角线,BE⊥AC,垂足为E;DF⊥AC,垂足为F.