题目内容
如图①,有一张菱形纸片ABCD,AC=8,BD=6.

(1)请沿着AC剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图②中用实线画出你所拼成的平行四边形;
(2)若沿着BD剪开,请在图③中用实线画出拼成的平行四边形;
(3)并直接写出这两个平行四边形的周长.图②中周长为 图③中周长为
(注:上述所画的平行四边形都不能与原菱形全等)

(1)请沿着AC剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四边形,在图②中用实线画出你所拼成的平行四边形;
(2)若沿着BD剪开,请在图③中用实线画出拼成的平行四边形;
(3)并直接写出这两个平行四边形的周长.图②中周长为
(注:上述所画的平行四边形都不能与原菱形全等)
考点:图形的剪拼,平行四边形的性质,菱形的性质
专题:
分析:(1)利用菱形的性质以及平行四边形的性质拼凑图案,即可得出答案;
(2)利用菱形的性质以及平行四边形的性质拼凑图案,即可得出答案;
(3)根据平行四边形的性质以及菱形性质得出各边长度.
(2)利用菱形的性质以及平行四边形的性质拼凑图案,即可得出答案;
(3)根据平行四边形的性质以及菱形性质得出各边长度.
解答:解:(1)如图②所示:
 ;
;
(2)如图③所示:

(3)如图②,∵菱形纸片ABCD,AC=8,BD=6,
根据菱形的对角线垂直且互相平分得出,
∴AB=BC=CD=AD=5,AC=BE=8,
∴AB+CE+AC+BE=8+5+5+8=26;
如图③:BD=CF=6,CD=BF=5,
得出BD+BF+DC+CF=22.
故答案为:26,22.
 ;
;(2)如图③所示:

(3)如图②,∵菱形纸片ABCD,AC=8,BD=6,
根据菱形的对角线垂直且互相平分得出,
∴AB=BC=CD=AD=5,AC=BE=8,
∴AB+CE+AC+BE=8+5+5+8=26;
如图③:BD=CF=6,CD=BF=5,
得出BD+BF+DC+CF=22.
故答案为:26,22.
点评:此题主要考查了菱形的性质以及平行四边形的性质以及图形的剪拼,根据图形对应边之间关系进行剪拼是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为6和8.设点P到AC的距离为x,到BD的距离为y,则x+y的值是( )
如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为6和8.设点P到AC的距离为x,到BD的距离为y,则x+y的值是( )A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
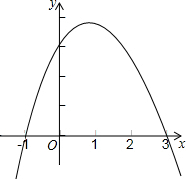 二次函数y=ax2+bx+c(a、b、c是常数a≠0)的大致图象如图所示,抛物线交x轴于点(-1,0),(3,0).则下列说法中,正确的是( )
二次函数y=ax2+bx+c(a、b、c是常数a≠0)的大致图象如图所示,抛物线交x轴于点(-1,0),(3,0).则下列说法中,正确的是( )| A、abc>0 |
| B、b-2a=0 |
| C、3a+c>0 |
| D、9a+6b+4c>0 |
已知点P(2a-3,a+1)在第二象限,则a的取值范围是( )
A、a>
| ||
| B、a<-1 | ||
C、-1<a<
| ||
D、1<a<
|
 如图,在△ABC和△PQD中,
如图,在△ABC和△PQD中, 如图,点B在反比例函数
如图,点B在反比例函数