题目内容
已知某几何体的三视图如图所示，则该几何体的体积为（ ）A、
| ||
| B、3π | ||
C、
| ||
| D、6π |
考点：由三视图判断几何体
专题：
分析：通过三视图判断几何体的特征，利用三视图的数据，求出几何体的体积即可．
解答：
解：由三视图可知几何体是圆柱底面半径为1高为6的圆柱，被截的一部分，如图
所求几何体的体积为：
×π×12×6=3π．
故选B．
解：由三视图可知几何体是圆柱底面半径为1高为6的圆柱，被截的一部分，如图所求几何体的体积为：
| 1 |
| 2 |
故选B．
点评：本题考查三视图与几何体的关系，正确判断几何体的特征是解题的关键，考查计算能力．
练习册系列答案
相关题目
如图，点P是矩形ABCD的边AD的一个动点，矩形的两条边AB、BC的长分别为6和8．设点P到AC的距离为x，到BD的距离为y，则x+y的值是（ ）A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
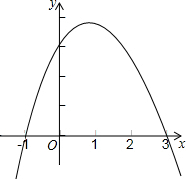二次函数y=ax2+bx+c（a、b、c是常数a≠0）的大致图象如图所示，抛物线交x轴于点（-1，0），（3，0）．则下列说法中，正确的是（ ）| A、abc＞0 |
| B、b-2a=0 |
| C、3a+c＞0 |
| D、9a+6b+4c＞0 |
如图，抛物线y=ax2+bx+c经过点（-1，0），对称轴为x=1；现有：已知点P（2a-3，a+1）在第二象限，则a的取值范围是（ ）
A、a＞
| ||
| B、a＜-1 | ||
C、-1＜a＜
| ||
D、1＜a＜
|
已知⊙O1，⊙O2的半径是2，4，圆心距为2，则这两圆的位置关系为（ ）
| A、外切 | B、内含 | C、相交 | D、内切 |