题目内容
如图，⊙O的半径为5，AB为⊙O的弦，OC⊥AB于点C．若OC=3，则AB的长为（ ）| A、4 | B、6 | C、8 | D、10 |
考点：垂径定理,勾股定理
专题：
分析：连接OA，先根据勾股定理求出AC的长，再由垂径定理可知AB=2AC，故可得出结论．
解答：
解：连接OA，
∵OC⊥AB，OA=5，OC=3，
∴AC=
=
=4，
∵OC过圆心，
∴AB=2AC=2×4=8．
故选C．
解：连接OA，∵OC⊥AB，OA=5，OC=3，
∴AC=
| OA2-OC2 |
| 52-32 |
∵OC过圆心，
∴AB=2AC=2×4=8．
故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
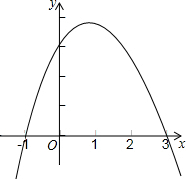二次函数y=ax2+bx+c（a、b、c是常数a≠0）的大致图象如图所示，抛物线交x轴于点（-1，0），（3，0）．则下列说法中，正确的是（ ）| A、abc＞0 |
| B、b-2a=0 |
| C、3a+c＞0 |
| D、9a+6b+4c＞0 |
如图，点B在反比例函数已知⊙O1，⊙O2的半径是2，4，圆心距为2，则这两圆的位置关系为（ ）
| A、外切 | B、内含 | C、相交 | D、内切 |
如图，Rt△ABC的斜边AC的两个顶点在反比例函数