题目内容
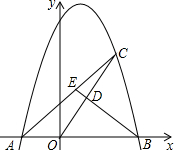 如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.(1)说明:
| CE |
| AE |
| 2 |
| 3 |
(2)当点C、点A到y轴距离相等时,求点E坐标;
(3)当△CDE的面积为
| 8 |
| 5 |
考点:二次函数综合题
专题:
分析:(1)由抛物线y=-x2+2x+8与x轴交于A、B两点,即可求得点A与B的坐标,然后过点O作OG∥AC交BE于点G,可得△CED∽△OGD,△BOG∽△BAE,然后由相似三角形的对应边成比例,得到CE=OG,继而证得
=
;
(2)由点C、点A到y轴距离相等,可得点C的横坐标为2,然后代入y=-x2+2x+8,即可求得点E坐标;
(3)首先连接OE,过点C作CF⊥AB于点F,由
=
,易得
=
.则可求得CF的长,继而求得点C的坐标,则可求得tan∠CAB的值.
| CE |
| AE |
| 2 |
| 3 |
(2)由点C、点A到y轴距离相等,可得点C的横坐标为2,然后代入y=-x2+2x+8,即可求得点E坐标;
(3)首先连接OE,过点C作CF⊥AB于点F,由
| CE |
| AE |
| 2 |
| 3 |
| S△CED |
| S△AOC |
| 1 |
| 5 |
解答: (1)证明:∵抛物线y=-x2+2x+8与x轴交于A、B两点,
(1)证明:∵抛物线y=-x2+2x+8与x轴交于A、B两点,
当y=0时,-x2+2x+8=0,
解得:x1=4,x2=-2,
∴点A(-2,0),B(4,0),
∴OB=4,AB=6,
过点O作OG∥AC交BE于点G.
∴△CED∽△OGD,
∴
=
;
∵点D是OC的中点,即DC=DO,
∴CE=OG;
∵OG∥AC,
∴△BOG∽△BAE,
∴
=
.
∴
=
=
=
=
.
(2)解:∵点C、点A到y轴距离相等,
∴点C的横坐标为2,
∴y=-22+2×2+8=8,
∴点C的坐标为:(2,8),A(-2,0),
设直线AC的解析式为y=kx+b(k≠0),
则
,解得
,
∴直线AC的解析式为y=2x+4,
∵点D是线段OC的中点,
∴D(1,4),
∵B(4,0),
∴设直线BD的解析式为y=ax+c(a≠0),
∴
,解得
,
∴直线BD的解析式为y=-
x+
,
∵
,解得
,
∴E(
,
);
(3)解:连接OE,过点C作CF⊥AB于点F.
∵D是OC的中点,
 ∴S△OCE=2S△CED,
∴S△OCE=2S△CED,
∵
=
,
∴
=
,
∵
=
=
,
∴
=
.
∴S△AOC=5S△CED=5×
=8,
∵S△AOC=
OA•CF=
×2×CF=CF,
∴CF=8,
∴当y=8时,8=-x2+2x+8,
解得:x1=0,x2=2,
∴点C的坐标为:(2,8),
∴AF=4,
∴tan∠CAB=
=
=2.
 (1)证明:∵抛物线y=-x2+2x+8与x轴交于A、B两点,
(1)证明:∵抛物线y=-x2+2x+8与x轴交于A、B两点,当y=0时,-x2+2x+8=0,
解得:x1=4,x2=-2,
∴点A(-2,0),B(4,0),
∴OB=4,AB=6,
过点O作OG∥AC交BE于点G.
∴△CED∽△OGD,
∴
| DC |
| DO |
| CE |
| OG |
∵点D是OC的中点,即DC=DO,
∴CE=OG;
∵OG∥AC,
∴△BOG∽△BAE,
∴
| OG |
| AE |
| OB |
| AB |
∴
| CE |
| AE |
| OG |
| AE |
| OB |
| AB |
| 4 |
| 6 |
| 2 |
| 3 |
(2)解:∵点C、点A到y轴距离相等,
∴点C的横坐标为2,
∴y=-22+2×2+8=8,

∴点C的坐标为:(2,8),A(-2,0),
设直线AC的解析式为y=kx+b(k≠0),
则
|
|
∴直线AC的解析式为y=2x+4,
∵点D是线段OC的中点,
∴D(1,4),
∵B(4,0),
∴设直线BD的解析式为y=ax+c(a≠0),
∴
|
|
∴直线BD的解析式为y=-
| 4 |
| 3 |
| 16 |
| 3 |
∵
|
|
∴E(
| 2 |
| 5 |
| 24 |
| 5 |
(3)解:连接OE,过点C作CF⊥AB于点F.
∵D是OC的中点,
 ∴S△OCE=2S△CED,
∴S△OCE=2S△CED,∵
| CE |
| AE |
| 2 |
| 3 |
∴
| CE |
| CA |
| 2 |
| 5 |
∵
| S△OCE |
| S△AOC |
| CE |
| CA |
| 2 |
| 5 |
∴
| S△CED |
| S△AOC |
| 1 |
| 5 |
∴S△AOC=5S△CED=5×
| 8 |
| 5 |
∵S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=8,
∴当y=8时,8=-x2+2x+8,
解得:x1=0,x2=2,
∴点C的坐标为:(2,8),
∴AF=4,
∴tan∠CAB=
| CF |
| AF |
| 8 |
| 4 |
点评:此题考查了二次函数的性质以及相似三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
在一次射击中,甲、乙两人5次射击的成绩分别如下:(单位:环)
甲:10,8,10,10,7 乙:7,9,9,10,10
这次射击中,甲、乙二人方差大小关系为( )
甲:10,8,10,10,7 乙:7,9,9,10,10
这次射击中,甲、乙二人方差大小关系为( )
A、S
| ||||
B、S
| ||||
C、S
| ||||
| D、无法确定 |
 如图所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.
如图所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.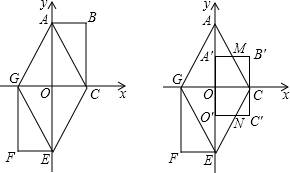
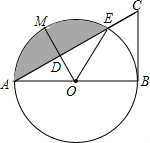 如图,以线段AB为直径的⊙O交线段AC于点E,点M是
如图,以线段AB为直径的⊙O交线段AC于点E,点M是