题目内容
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1800,得到矩形OEFG,顺次连接AC、CE、EG、GA.
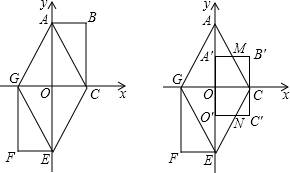
(1)请直接写出点F的坐标;
(2)试判断四边形ACEG的形状,并说明理由;
(3)将矩形OABC沿y轴向下平移m个单位(0<m<4),设平移过程中矩形与△AEC重叠部分面积为S1,当S1:S△AEC=11:16时,求m的值.

(1)请直接写出点F的坐标;
(2)试判断四边形ACEG的形状,并说明理由;
(3)将矩形OABC沿y轴向下平移m个单位(0<m<4),设平移过程中矩形与△AEC重叠部分面积为S1,当S1:S△AEC=11:16时,求m的值.
考点:四边形综合题
专题:
分析:(1)根据A、B的坐标和矩形的性质,旋转的性质即可得出OC=OG=AB=2,BC=FG=4,即可得出答案;
(2)根据旋转的性质得出OA=OE,OC=OG,得出平行四边形,根据AE⊥CG即可得出答案;
(3)求出S△AA′M+S△EO′N=
S△ACE,求出后代入得出关于m的方程,求出即可.
(2)根据旋转的性质得出OA=OE,OC=OG,得出平行四边形,根据AE⊥CG即可得出答案;
(3)求出S△AA′M+S△EO′N=
| 5 |
| 16 |
解答:解:(1)∵A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1800,得到矩形OEFG,
∴BC=FG=4,OC=AB=OG=2,
∴F(-2,-4);
(2)四边形ACEG是菱形,
理由:根据题意得:OA=OE,OC=OG,
∴四边形ACEG是平行四边形,
又∵AE⊥GC
∴四边形ACEG是菱形;
(3)如图,将矩形OABC沿y轴向下平移m个单位得到矩形O′A′B′C′,
则当S1:S△AEC=11:16时,重叠部分为五边形MCNO′A′,
∵S1:S△AEC=11:16,
∴S△AAM′+S△EON′=
S△AEC=
×8=
,
∵A′B′∥GC,
∴△AA′M∽△AOC,
∴
=
=2,
∴A′M=
AA′=
m,
∴S△AAM′=
×
m×m=
m2,
同理可得:S△EO′N=
(4-m)2,
∴
m2+
(4-m)2=
,
解得:m=1或m=3.
∴BC=FG=4,OC=AB=OG=2,
∴F(-2,-4);
(2)四边形ACEG是菱形,
理由:根据题意得:OA=OE,OC=OG,
∴四边形ACEG是平行四边形,
又∵AE⊥GC
∴四边形ACEG是菱形;
(3)如图,将矩形OABC沿y轴向下平移m个单位得到矩形O′A′B′C′,
则当S1:S△AEC=11:16时,重叠部分为五边形MCNO′A′,
∵S1:S△AEC=11:16,
∴S△AAM′+S△EON′=
| 5 |
| 16 |
| 5 |
| 16 |
| 5 |
| 2 |
∵A′B′∥GC,
∴△AA′M∽△AOC,
∴
| AA′ |
| A′M |
| AO |
| OC |
∴A′M=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AAM′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
同理可得:S△EO′N=
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 2 |
解得:m=1或m=3.
点评:本题考查了三角形面积,矩形的性质,菱形的判定,平行四边形的判定,旋转的性质,相似三角形的性质和判定的应用,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
函数y=4x-2与y=-4x-2的交点坐标为( )
| A、(-2,0) |
| B、(0,-2) |
| C、(0,2) |
| D、(2,0) |
 实数a、b在数轴上的位置如图所示,化简
实数a、b在数轴上的位置如图所示,化简
 如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作: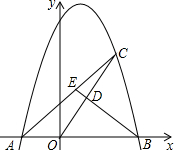 如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E. 如图,⊙M的圆心在x轴上,与坐标轴交于A(0,
如图,⊙M的圆心在x轴上,与坐标轴交于A(0,