题目内容
在一次射击中,甲、乙两人5次射击的成绩分别如下:(单位:环)
甲:10,8,10,10,7 乙:7,9,9,10,10
这次射击中,甲、乙二人方差大小关系为( )
甲:10,8,10,10,7 乙:7,9,9,10,10
这次射击中,甲、乙二人方差大小关系为( )
A、S
| ||||
B、S
| ||||
C、S
| ||||
| D、无法确定 |
考点:方差
专题:
分析:分别计算甲、乙的方差后比较即可.
解答:解:甲的平均数=(10+8+10+10+7)÷5=9
乙的平均数=(7+10+9+9+10)÷5=9
s甲2=
[(10-9)2+(8-9)2+(10-9)2+(10-9)2+(7-9)2]=1.6
s乙2=
[(7-9)2+(10-9)2+(10-9)2+(9-9)2+(9-9)2]=1.2
故选B.
乙的平均数=(7+10+9+9+10)÷5=9
s甲2=
| 1 |
| 5 |
s乙2=
| 1 |
| 5 |
故选B.
点评:本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
已知一次函数y=kx-k(k≠0),当k取不同的值时表示不同的函数.则下列说法正确的是( )
| A、不论k取何值,函数图象必过点(1,1) |
| B、不论k取何值,函数图象必过点(2,1) |
| C、不论k取何值,函数图象必过点(1,0) |
| D、不论k取何值,函数图象必过点(-l,1) |
设a,b,c是△ABC的三边长,二次函数y=(a-
)x2-cx-a-
在x=1时取最小值-
b,则△ABC是( )
| b |
| 2 |
| b |
| 2 |
| 8 |
| 5 |
| A、等腰三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、直角三角形 |
函数y=4x-2与y=-4x-2的交点坐标为( )
| A、(-2,0) |
| B、(0,-2) |
| C、(0,2) |
| D、(2,0) |
将正偶数按下表排成5列:
第1列 第2列 第3列 第4列 第5列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
第4行 32 30 28 26
…
根据上面的排列规律,则2000应在( )
第1列 第2列 第3列 第4列 第5列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
第4行 32 30 28 26
…
根据上面的排列规律,则2000应在( )
| A、第125行,第1列 |
| B、第125行,第2列 |
| C、第250行,第1列 |
| D、第250行,第2列 |
 在坡度为1:7的斜坡上,一个人从A点出发向上运动到点B,若AB=30m,则此人升高了( )m.
在坡度为1:7的斜坡上,一个人从A点出发向上运动到点B,若AB=30m,则此人升高了( )m.A、
| ||
B、
| ||
C、21
| ||
D、3
|
若4a-3b=7,3a+2b=19,则14a-2b是( )
| A、48 | B、52 | C、58 | D、60 |
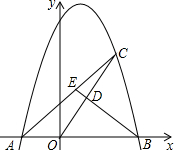 如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.