Question

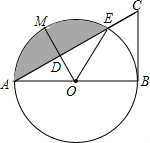如图，以线段AB为直径的⊙O交线段AC于点E，点M是

AE

的中点，OM交AC于点D，∠BOE=60°，cosC=

1

2

，BC=2

3

．
（1）求证：BC是⊙O的切线； 
（2）求阴影部分弓形的面积．

Answer 1

考点：切线的判定,扇形面积的计算

专题：

分析：（1）要证BC是⊙O的切线，只要证明AB⊥BC即可．
（2）根据切线的性质，运用三角函数的知识求出MD的长度，利用扇形的面积减去等腰三角形的面积即可求得阴影部分的面积．

解答：解：（1）证明：在△ABC中，∵cosC=

1

2

，
∴∠C=60°．
又∵∠A=30°，
∴∠ABC=90°，
∴AB⊥BC．（
∴BC是⊙O的切线．

（2）解：∵点M是

AE

的中点，
∴OM⊥AE．（1分）
在Rt△ABC中，∵BC=2

3

，
∴AB=BC•tan60°=2

3

×

3

=6．（2分）
∴OA=

AB

2

=3，
∴OD=

1

2

OA=

3

2

，
∴S_弓形=S_扇形-S_△AEO=

120×32π

360

-

1

2

×3

3

×

3

2

=3π-

9 3

4

．

点评：本题综合考查了三角函数的知识、切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．