题目内容
解不等式(组)
(1)4(x-2)+7<5(x-1)+6
(2)
.
(1)4(x-2)+7<5(x-1)+6
(2)
|
考点:解一元一次不等式组,解一元一次不等式
专题:计算题
分析:(1)先去括号,再移项、合并,然后把x的系数化为1即可;
(2)分别解两个不等式得到x<2和x≥-2,然后根据大于小的小于大的取中间确定不等式组的解集.
(2)分别解两个不等式得到x<2和x≥-2,然后根据大于小的小于大的取中间确定不等式组的解集.
解答:解:(1)4x-8+7<5x-5+6,
4x-5x<-5+6+8-7,
-x<2,
所以x>-2;
(2)
,
解①得x<2,
解②得x≥-2,
所以不等式组的解集为-2≤x<2.
4x-5x<-5+6+8-7,
-x<2,
所以x>-2;
(2)
|
解①得x<2,
解②得x≥-2,
所以不等式组的解集为-2≤x<2.
点评:本题考查了解一元一次不等式组:求解出两个不等式的解集,然后按照“同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解”确定不等式组的解集.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
将正偶数按下表排成5列:
第1列 第2列 第3列 第4列 第5列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
第4行 32 30 28 26
…
根据上面的排列规律,则2000应在( )
第1列 第2列 第3列 第4列 第5列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
第4行 32 30 28 26
…
根据上面的排列规律,则2000应在( )
| A、第125行,第1列 |
| B、第125行,第2列 |
| C、第250行,第1列 |
| D、第250行,第2列 |
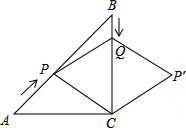 如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
 如图是某几何体的三视图.
如图是某几何体的三视图.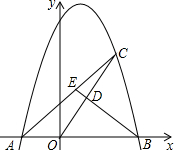 如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E. 如图,∠1=47°,∠2=47°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
如图,∠1=47°,∠2=47°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么? 如图,已知∠AOD和∠BOC都是直角,∠DOC=62°,求∠AOB的度数.
如图,已知∠AOD和∠BOC都是直角,∠DOC=62°,求∠AOB的度数.