题目内容
已知y=y1+y2,y1与x成正比例,y2与x成反比例,且x=1时,y=7,当x=2时,y=8.求:
(1)y与x之间的函数关系;
(2)自变量的取值范围;
(3)当x=4时y的取值.
(1)y与x之间的函数关系;
(2)自变量的取值范围;
(3)当x=4时y的取值.
考点:待定系数法求反比例函数解析式
专题:
分析:(1)根据y1与x成正比例,y2与x成反比例,可设y1=ax,y2=
,又y=y1+y2,得到y关于x的函数关系式,再进一步代入x,y的值得到方程组,从而求得函数关系式;
(2)根据反比例函数确定自变量的取值范围;
(3)将x=4代入函数解析式求得函数值即可.
| b |
| x |
(2)根据反比例函数确定自变量的取值范围;
(3)将x=4代入函数解析式求得函数值即可.
解答:解:(1)根据题意,设y1=ax,y2=
;
又y=y1+y2,则y=ax+
;
又当x=1时,y=7;
当x=2时,y=8.
得
,
解得
.
∴y关于x的函数解析式为:y=3x+
.
(2)自变量的取值范围为x≠0;
(3)当x=4时,y=3×4+1=13;
| b |
| x |
又y=y1+y2,则y=ax+
| b |
| x |
又当x=1时,y=7;
当x=2时,y=8.
得
|
解得
|
∴y关于x的函数解析式为:y=3x+
| 4 |
| x |
(2)自变量的取值范围为x≠0;
(3)当x=4时,y=3×4+1=13;
点评:此题首先根据题意分别建立y1与x,y2与x的函数关系式,再进一步得到y与x之间的函数关系式,然后代入得到关于a,b的方程组,从而求解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 在坡度为1:7的斜坡上,一个人从A点出发向上运动到点B,若AB=30m,则此人升高了( )m.
在坡度为1:7的斜坡上,一个人从A点出发向上运动到点B,若AB=30m,则此人升高了( )m.A、
| ||
B、
| ||
C、21
| ||
D、3
|
 实数a、b在数轴上的位置如图所示,化简
实数a、b在数轴上的位置如图所示,化简 如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作: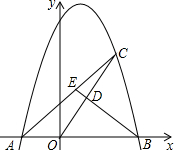 如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
如图,已知抛物线y=-x2+2x+8与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E. 如图,EF交AD于O,AB交AD于A,CD交AD于D,∠1=∠2,∠3=∠4,试判AB和CD的位置关系,并说明为什么.
如图,EF交AD于O,AB交AD于A,CD交AD于D,∠1=∠2,∠3=∠4,试判AB和CD的位置关系,并说明为什么. 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.
如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.