题目内容
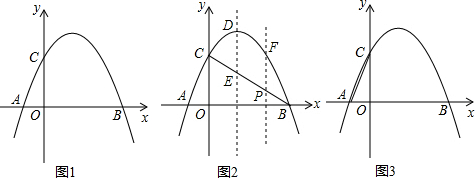
17. 已知反比例函数的两支图象关于原点对称,利用这一结论解决下列问题:如图,在同一直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).
已知反比例函数的两支图象关于原点对称,利用这一结论解决下列问题:如图,在同一直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).(1)填空:无论k取何值时,四边形ABCD的形状一定是平行四边形;
(2)①当点B为(p,1)时,四边形ABCD是矩形,试求p,k,和m的值;
②填空:对①中的m值,能使四边形ABCD为矩形的点B共有2个.
(3)四边形ABCD能不能是菱形?若能,直接写出B点的坐标;若不能,说明理由.
分析 (1)根据对称的性质可得四边形ABCD的对角线互相平分,则一定是平行四边形;
(2)①把B的坐标代入反比例函数的解析式即可求得p的值,利用待定系数法求得k的值,利用勾股定理求得m的值;
②根据反比例函数图象的对称性,在反比例函数图象上,连线经过O,且连线等于AC的一定有两组,据此即可判断;
(3)根据四边形ABCD的对角线一定不能垂直即可判断.
解答 解:(1)根据对称性可得:OA=OC,OB=OD,则四边形ABCD是平行四边形.
故答案是:平行四边形;
(2)①∵点B(p,1)在y=$\frac{\sqrt{3}}{x}$上,
∴1=$\frac{\sqrt{3}}{p}$,解得p=$\sqrt{3}$.
把B($\sqrt{3}$,1)代入y=kx得k=$\frac{\sqrt{3}}{3}$.
∵OB2=($\sqrt{3}$)2+12=4,
∴OB=2.
∵正比例函数、反比例函数的图象都关于原点对称,
∴OA=OB=OC=2,
∴m=2;
② 作出第一、三象限的角的平分线,交反比例函数图象于点M、N.则MN的解析式是y=x.
作出第一、三象限的角的平分线,交反比例函数图象于点M、N.则MN的解析式是y=x.
当x=m=2时,反比例函数上对应的点是(2,$\frac{\sqrt{3}}{2}$),
直线y=x上对应的点是(2,2).
∵2>$\frac{\sqrt{3}}{2}$,
∴(2,$\frac{\sqrt{3}}{2}$)在OM的延长线上,即MN<AC.
则能使四边形ABCD是矩形的点B共有2个,
故答案是:2;
(3)四边形ABCD不能是菱形.
理由是:∵A(-m,0)、C(m,0),
∴四边形ABCD的对角线AC在x轴上,
又∵点B、D分别是正比例函数与反比例函数在第一、三象限的交点,
∴对角线BD和AC不可能垂直.
∴四边形ABCD不可能是菱形.
点评 本题考查了反比例函数的图象的对称性以及菱形的判定,正确理解正比例函数与反比例函数关于原点对称是关键.

| A. | -5 | B. | 0 | C. | $\sqrt{8}$ | D. | 3 |
 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )| A. | 40海里 | B. | 40$\sqrt{2}$海里 | C. | 40$\sqrt{3}$海里 | D. | 40$\sqrt{6}$海里 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
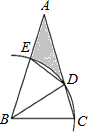 如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )| A. | 2$\sqrt{3}$+2-$\frac{5}{6}$π | B. | $\sqrt{3}$+1-$\frac{5}{3}$π | C. | 2$\sqrt{3}$+2-$\frac{1}{2}$π | D. | $\sqrt{3}$+1-$\frac{1}{2}$π |
| A. | x2+x2=x4 | B. | (-a2)3=-a6 | C. | (a-b)2=a2-b2 | D. | 3a2•2a3=6a6 |