题目内容
18．
如图，△ABC中，∠BAC=90°，沿AD折叠△ABD，使点B恰好落在AC边上的点E处．若∠C=24°，则∠ADE等于（ ）| A． | 66° | B． | 69° | C． | 70° | D． | 71° |
分析 根据三角形内角和定理求出∠B的度数，根据翻折变换的性质求出∠EAD的度数，根据三角形内角和定理求出∠ADE．
解答 解：在△ABC中，∠CAB=90°，∠C=24°，
∴∠B=90°-∠C=66°．
由折叠的性质可得：∠EAD=$\frac{1}{2}$∠CAB=45°，
∴∠ADE=180°-∠EAD-∠B
=69°．
故选：B
点评 本题考查的是翻折变换和三角形内角和定理，理解翻折变换的性质、熟记三角形内角和等于180°是解题的关键．
练习册系列答案
相关题目
9．现定义运算“△”，对于任意有理数a、b，都有a△b=a2-ab+b，例如：3△5=32-3×5+5=11，由此算出（x-1）△（2+x）等于（ ）
| A． | 2x-5 | B． | 2x-3 | C． | -2x+5 | D． | -2x+3 |
6．
如图是一个标注了角度和尺寸工件的模型，则此工件的面积用a，b表示为（ ）
如图是一个标注了角度和尺寸工件的模型，则此工件的面积用a，b表示为（ ）| A． | $\frac{1}{2}{a}^{2}$-$\frac{1}{2}$ab+$\frac{1}{2}$b2 | B． | $\frac{1}{2}{a}^{2}$-$\frac{1}{2}$ab+b2 | C． | $\frac{1}{2}{a}^{2}$+$\frac{1}{2}$ab+b2 | D． | a2-ab+b2 |
13．
如图，△ABC，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC=132°，∠BGC=118°，则∠A的度数为（ ）
如图，△ABC，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC=132°，∠BGC=118°，则∠A的度数为（ ）| A． | 65° | B． | 66° | C． | 70° | D． | 78° |
如图所示的运算程序中，若开始输入的x值为10，我们发现第1次输出的结果为5，第2次输出的结果为8，…，第2016次输出的结果为4．
7．某商品的标价为800元，4折销售仍可赚60元，则该商品的进价为（ ）
| A． | 92元 | B． | 260元 | C． | 320元 | D． | 740元 |
8．
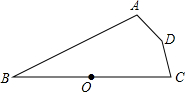如图，O是线段BC的中点，A、D、C到O点的距离相等，若∠ABC=30°，则∠ADC的度数是（ ）
如图，O是线段BC的中点，A、D、C到O点的距离相等，若∠ABC=30°，则∠ADC的度数是（ ）| A． | 150° | B． | 120° | C． | 60° | D． | 30° |