题目内容
8．
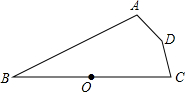如图，O是线段BC的中点，A、D、C到O点的距离相等，若∠ABC=30°，则∠ADC的度数是（ ）| A． | 150° | B． | 120° | C． | 60° | D． | 30° |
分析 根据题意得到四边形ABCD共圆，利用圆内接四边形对角互补即可求出所求角的度数．
解答 
解：由题意得到OA=OB=OC=OD，作出圆O，如图所示，
∴四边形ABCD为圆O的内接四边形，
∴∠ABC+∠ADC=180°，
∵∠ABC=30°，
∴∠ADC=150°，
故选A
点评 此题考查了圆内接四边形的性质，熟练掌握圆内接四边形的性质是解本题的关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
18．
如图，△ABC中，∠BAC=90°，沿AD折叠△ABD，使点B恰好落在AC边上的点E处．若∠C=24°，则∠ADE等于（ ）
如图，△ABC中，∠BAC=90°，沿AD折叠△ABD，使点B恰好落在AC边上的点E处．若∠C=24°，则∠ADE等于（ ）| A． | 66° | B． | 69° | C． | 70° | D． | 71° |
19．
如图，在Rt△ABC中∠C=90°，点P、Q同时由A、B两点出发分别沿AC、BC方向向C点匀速运动，其速度为2m/s，几秒后△PCQ的面积是△ABC面积的一半（ ）
如图，在Rt△ABC中∠C=90°，点P、Q同时由A、B两点出发分别沿AC、BC方向向C点匀速运动，其速度为2m/s，几秒后△PCQ的面积是△ABC面积的一半（ ）| A． | 1.5 | B． | 9 | C． | 1.5或9 | D． | 10 |
16．
如图，直线a，b相交于点O，若∠1等于45°，则∠2等于（ ）
如图，直线a，b相交于点O，若∠1等于45°，则∠2等于（ ）| A． | 45° | B． | 55° | C． | 115° | D． | 135° |
如图，学校有一块长方形花坛，有极少数人为了避开拐角走“捷径”，在花坛内走出了一条“路”，他们仅仅少走了（ ）步，却踩伤了花草（假设2步为1米）
13．用规格为50cm×50cm的地板砖密铺客厅恰好需要60块．若改用规格为xcm×xcm的地板砖y块，恰好也能将客厅铺完（不考虑铺设地砖之间的缝隙），那么y与x之间的关系为（ ）
| A． | y=$\frac{150000}{x}$ | B． | y=$\frac{150000}{{x}^{2}}$ | C． | y=150000x | D． | y=150000x2 |
20．下列哪个数与-3的乘积等于1（ ）
| A． | -3 | B． | 3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |
17．
如图，已知点A（3，4），点B为直线x=-2上的动点，点C（x，0）且-2＜x＜3，BC⊥AC垂足为点C，连接AB．若AB与y轴正半轴的所夹锐角为α，当tanα的值最大时x的值为（ ）
如图，已知点A（3，4），点B为直线x=-2上的动点，点C（x，0）且-2＜x＜3，BC⊥AC垂足为点C，连接AB．若AB与y轴正半轴的所夹锐角为α，当tanα的值最大时x的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$$\sqrt{3}$ | C． | 1 | D． | $\frac{1}{3}$ |