题目内容
计算:
(1)a3•(-b3)2+(-
ab2)3;
(2)(-2p-q)(-q+2p);
(3)(3-4y)(4y+3)+(-3-4y)2;
(4)已知a+a-1=3,求a4+
的值.
(1)a3•(-b3)2+(-
| 1 |
| 2 |
(2)(-2p-q)(-q+2p);
(3)(3-4y)(4y+3)+(-3-4y)2;
(4)已知a+a-1=3,求a4+
| 1 |
| a4 |
考点:整式的混合运算,负整数指数幂
专题:
分析:(1)先算乘方,再算乘法,再合并同类项即可;
(2)根据平方差公式展开,再求出即可;
(3)先根据平方差公式和完全平方公式展开,再合并即可;
(4)根据完全平方公式求出a2+a-2的值,再根据完全平方公式求出即可.
(2)根据平方差公式展开,再求出即可;
(3)先根据平方差公式和完全平方公式展开,再合并即可;
(4)根据完全平方公式求出a2+a-2的值,再根据完全平方公式求出即可.
解答:解:(1)原式=a3•b6+(-
a3b6)
=a3b6-
a3b6
=
a3b6;
(2)原式=(-q)2-(2p)2
=q2-4p2;
(3)原式=9-16y2+9+24y+16y2
=18+24y;
(4)∵a+a-1=3,
∴a2+a-2=(a+a-1)2-2•a•a-1=32-2=7,
∴a4+
=(a2+a-2)2-2•a2•a-2=72-2=47.
| 1 |
| 8 |
=a3b6-
| 1 |
| 8 |
=
| 7 |
| 8 |
(2)原式=(-q)2-(2p)2
=q2-4p2;
(3)原式=9-16y2+9+24y+16y2
=18+24y;
(4)∵a+a-1=3,
∴a2+a-2=(a+a-1)2-2•a•a-1=32-2=7,
∴a4+
| 1 |
| a4 |
点评:本题考查了整式的混合运算和求值,平方差公式,完全平方公式的应用,主要考查学生的化简能力和计算能力,题目比较好,难度适中.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )| A、6 | B、8 | C、10 | D、12 |

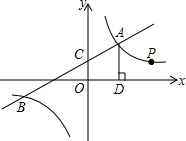 如图,一次函数y1=k1x+2与反比例函数y2=
如图,一次函数y1=k1x+2与反比例函数y2= 如图,在菱形ABCD中,∠DAB与∠ABC的度数比为1:2,周长是48cm.求:AC和BD的长度.
如图,在菱形ABCD中,∠DAB与∠ABC的度数比为1:2,周长是48cm.求:AC和BD的长度. 已知:如图,∠ADC=117°.试求∠A+∠B+∠C的度数.
已知:如图,∠ADC=117°.试求∠A+∠B+∠C的度数. 如图,已知将一矩形纸片ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E,已知AD=8cm,AB=4cm,求重叠部分△BED的面积.
如图,已知将一矩形纸片ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E,已知AD=8cm,AB=4cm,求重叠部分△BED的面积.