题目内容
11.一等腰三角形的腰长与底边之比为5:6,它底边上的高为$\sqrt{68}$,求这个等腰三角形的周长与面积.分析 根据题意画出图形,设腰长是5x,底边长是6x,根据等腰三角形三线合一的性质可得到其底边的一半的长,再利用勾股定理列方程,解方程即可求得腰长与底边的长,从而不难求得周长与面积的值.
解答 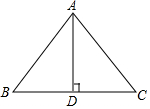 解:如图,∵AB=AC,AB:BC=5:6,
解:如图,∵AB=AC,AB:BC=5:6,
∴设AB=5x,则BC=6x.
∵AD⊥BC,AD=$\sqrt{68}$,
∴BD=3x.
∴BD2+AD2=AB2,即(3x)2+($\sqrt{68}$)2=(5x)2,解得x=2,
∴AB=10,BC=12,
∴C△ABC=2AB+BC=20+12=32;
S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×12×$\sqrt{68}$=12$\sqrt{17}$.
点评 此题考查的是勾股定理、等腰三角形及直角三角形的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
14.立方得8的数是( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 4或-4 |
20.已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.且a+b-c=m,①填表:②观察下表猜想:m×l=4S.(用含s的代数式表示)③证明②中的结论.
| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
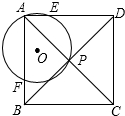 如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB、AD于点F、E.若⊙O的半径为$\frac{{\sqrt{3}}}{2}$,AB=$\sqrt{2}$+1,则$\frac{AE}{ED}$的值为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
如图,四边形ABCD为正方形,⊙O过正方形的顶点A和对角线的交点P,分别交AB、AD于点F、E.若⊙O的半径为$\frac{{\sqrt{3}}}{2}$,AB=$\sqrt{2}$+1,则$\frac{AE}{ED}$的值为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$. 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0). 如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E
如图,在△ABC中,∠ABE=2∠C,AD是∠BAC的平分线,BE⊥AD,垂足为E 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.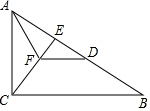 如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.
如图,在△ABC中,∠ACB=90°,CE是AB边上的高,AF平分∠CAB交CE于点F,过点F作FD∥CB交AB于点D.求证:AC=AD.