题目内容
10.已知,在等腰三角形ABC中,AB=BC,BD⊥AC于点D,以BC为边作等边△PBC,连接AP交BD所在直线于点Q,连接CQ.(1)如图1,若DQ=2,求CQ的长;
(2)如图1,求证:BD=QD-PQ;
(3)如图2,当点Q在线段BD上时,连接BC交AP于点H,若AB=$\sqrt{31}$,AQ=5,请直接写出HQ的长.

分析 (1)如图1中,以B为圆心BC为半径作⊙B.由BC=BA=BP,△BCP是等边三角形,推出∠CBP=60°,推出∠CAP=$\frac{1}{2}$∠CBP=30°,由此即可解决问题.
(2)如图2中,在DQ上取一点M,使得DM=DB.只要证明△CQP≌△CQM,推出PQ=QM,即可推出BD=DM=DQ-QM=DQ-PQ.
(3)如图3中,以BC为半径作⊙B,延长QD到M,使得DM=DQ,连接CM、AM.只要证明HQ∥CM,得$\frac{HQ}{CM}$=$\frac{BQ}{BM}$,求出CM、BQ、BM即可解决问题.
解答 (1)解:如图1中,以B为圆心BC为半径作⊙B.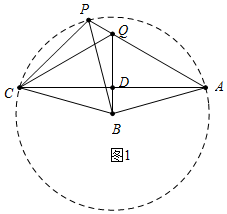
∵BC=BA=BP,△BCP是等边三角形,
∴∠CBP=60°,
∴∠CAP=$\frac{1}{2}$∠CBP=30°,
∵BQ⊥AC,
∴∠ADQ=90°,CD=AQ,
∴CQ=AQ,
∵DQ=2,
∴AQ=2DQ=4,
∴CQ=AQ=4.
(2)证明:如图2中,在DQ上取一点M,使得DM=DB.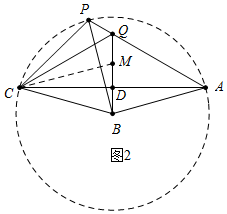
∵CD⊥BM,DM=BD,
∴CM=CB=CP,
∴∠DCM=∠DCB,
∵∠PCB=60°,∠QCD=∠CAQ=30°,
∴∠BCD+∠PCQ=30°=∠QCM+∠MCD,
∴∠QCP=∠QCM,
在△CQP和△CQM中,
$\left\{\begin{array}{l}{CQ=CQ}\\{∠QCP=∠QCM}\\{CP=CM}\end{array}\right.$,
∴△CQP≌△CQM,
∴PQ=QM,
∴BD=DM=DQ-QM=DQ-PQ,
∴BD=DQ-PQ
(3)解:如图3中,以BC为半径作⊙B,延长QD到M,使得DM=DQ,连接CM、AM.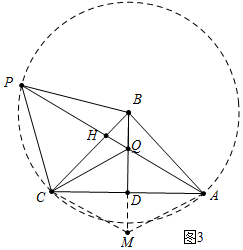
∵CD=AD,DQ=DM,
∴四边形CQAM是平行四边形,
∵QC=QA,
∴四边形CQAM是菱形,
∴CM=AQ=5,
在Rt△ADQ中,∵∠ADQ=90°,∠QAD=30°,AQ=5,
∴DQ=$\frac{5}{2}$,AD=$\frac{5}{2}$$\sqrt{3}$,
在Rt△ABD中,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{(\sqrt{31})^{2}-(\frac{5}{2}\sqrt{3})^{2}}$=$\frac{7}{2}$,
∴BQ=BD-DQ=$\frac{7}{2}$-$\frac{5}{2}$=1,BM=$\frac{7}{2}$+$\frac{5}{2}$=6,
∵HQ∥CM,
∴$\frac{HQ}{CM}$=$\frac{BQ}{BM}$,
∴$\frac{HQ}{5}$=$\frac{1}{6}$,
∴HQ=$\frac{5}{6}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、圆周角定理、等边三角形的性质、勾股定理、直角三角形30度角性质、平行线分线段成比例定理等知识,解题的关键是学会添加辅助圆,构造全等三角形解决问题,属于中考压轴题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
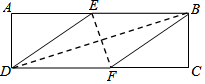 在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE,现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )| A. | ①是假命题,②是假命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①是真命题,②是真命题 |
| A. | 1,2,$\sqrt{3}$ | B. | 3,4,5 | C. | 1,1,$\sqrt{2}$ | D. | 6,12,13 |
| A. |  | B. |  | ||
| C. | 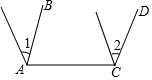 | D. | 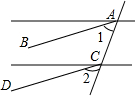 |
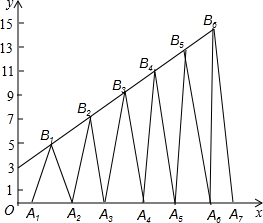 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a. 如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.
如图,已知△ABC,请用尺规作△ABC的中位线EF,使EF∥BC.