题目内容
5.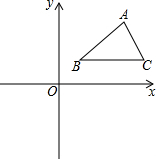 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).(1)若点K以每秒移动$\frac{1}{2}$个单位长度的速度,从点C出发,沿射线CB方向运动,当AK恰好将△ABC的面积平分时,求点K运动的时间.
(2)若点K从点C出发,沿射线CB方向运动6秒时,当△AKB的面积为△ABC面积的$\frac{2}{3}$,求点K的运动速度.
分析 (1)设点K运动的时间为t,知CK=$\frac{1}{2}$t,由“AK恰好将△ABC的面积平分”知S△ACK=$\frac{1}{2}$S△ABC,据此列方程求解可得;
(2)设点K的运动速度为x单位/秒,则CK=6x,分点K在BC上和点K在BC延长线上两种情况,依据S△AKB=$\frac{2}{3}$S△ABC列方程求解可得.
解答 解:(1)设点K运动的时间为t,
则CK=$\frac{1}{2}$t,
∵A(8,6),B(3,2),C(9,2).
∴BC=6,AD=4,
∵AK恰好将△ABC的面积平分,即S△ACK=$\frac{1}{2}$S△ABC,
∴$\frac{1}{2}$×$\frac{1}{2}$t×4=$\frac{1}{2}$×$\frac{1}{2}$×6×4,
解得t=6,
答:点K的运动时间为6秒;
(2)设点K的运动速度为x单位/秒,
则CK=6x,
当点K在BC上时,BK=6-6x,
由S△AKB=$\frac{2}{3}$S△ABC得$\frac{1}{2}$×(6-6x)×4=$\frac{2}{3}$×$\frac{1}{2}$×6×4,
解得:x=$\frac{1}{3}$;
当点K在BC延长线上时,BK=6x-6,
由S△AKB=$\frac{2}{3}$S△ABC得$\frac{1}{2}$×(6x-6)×4=$\frac{2}{3}$×$\frac{1}{2}$×6×4,
解得:x=$\frac{5}{3}$;
答:K的运动速度为$\frac{1}{3}$或$\frac{5}{3}$个单位/秒.
点评 本题主要考查坐标与图形的性质、一元一次方程的应用及分类讨论思想的运用,根据面积之间的关系列出方程是解题的关键.

练习册系列答案
相关题目
8.下列方程中,属于一元一次方程的是( )
| A. | x+2y=1 | B. | 2y+$\frac{y}{2}$+1=0 | C. | $\frac{2}{x}$+3=0 | D. | 2y2=8 |
20.已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.且a+b-c=m,①填表:②观察下表猜想:m×l=4S.(用含s的代数式表示)③证明②中的结论.
| 三边a、b、c | m | l×m | S |
| 3、4、5 | 2 | 24 | 6 |
| 5、12、13 | 4 | 120 | 30 |
| 8、15、17 | 6 | 240 | 60 |
15.下列几组数据中,不可以作为直角三角形的三条边的是( )
| A. | 1,2,$\sqrt{3}$ | B. | 3,4,5 | C. | 1,1,$\sqrt{2}$ | D. | 6,12,13 |
 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.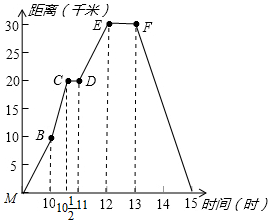 如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:
如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题: