题目内容
19.用配方法解方程:2x2-3x-3=0.分析 首先把方程的二次项系数化为1,移项,然后在方程的左右两边同时加上一次项系数一半的平方,左边就是完全平方式,右边就是常数,然后利用平方根的定义即可求解.
解答 解:2x2-3x-3=0,
x2-$\frac{3}{2}$x-$\frac{3}{2}$=0,
x2-$\frac{3}{2}$x+$\frac{9}{16}$=$\frac{9}{16}$+$\frac{3}{2}$,
(x-$\frac{3}{4}$)2=$\frac{33}{16}$,
x-$\frac{3}{4}$=±$\frac{\sqrt{33}}{4}$,
解得:x1=$\frac{3+\sqrt{33}}{4}$,x2=$\frac{3-\sqrt{33}}{4}$.
点评 此题考查利用配方法解一元二次方程,用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列各式从左到右的变形正确的是( )
| A. | $\frac{0.2a+b}{a+0.2b}=\frac{2a+b}{a+2b}$ | B. | $\frac{a+b}{a-b}=-\frac{a-b}{a+b}$ | ||
| C. | $\frac{20x+y}{50x-y}=\frac{2+y}{5x-y}$ | D. | $-\frac{x+1}{x-y}=\frac{x+1}{y-x}$ |
7.化简(x-1-1)-1的结果是( )
| A. | $\frac{x}{1-x}$ | B. | $\frac{x}{x-1}$ | C. | x-1 | D. | 1-x |
8.抛物线y=a1x2+b1x+c1绕点(0,2)旋转180°得到抛物线y=a2x2+b2x+c2,则下面等式成立的是( )
| A. | a1-a2=0 | B. | b1+b2=0 | C. | c1+c2=4 | D. | $\frac{{b}_{1}}{{a}_{1}}$=$\frac{{b}_{2}}{{a}_{2}}$ |
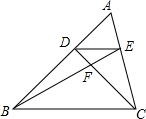 如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$.
如图,已知D、E分别是△ABC的边AB和AC上的点,DE∥BC,BE与CD相交于点F,如果AE=1,CE=2,那么EF:BF等于$\frac{1}{3}$. 如图所示,数轴的单位长度为1.
如图所示,数轴的单位长度为1. 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )