题目内容
2．
四边形ABCD在平面直角坐标系中的位置如图所示，若AB⊥AD，AB∥CD，且AB=5，A点坐标为（-2，7），则B点坐标为（3，7）．
分析 由题意知AB∥x轴，得出A、B两点纵坐标相同，由A点横坐标为-2，AB=5，点B在第一象限，所以点B横坐标为3，即可求出点B坐标．
解答 解：∵AB∥CD，
∴AB∥x轴，
∴A、B两点纵坐标相同为7，
∵AB∥x轴，AB=5，点B在第一象限，
∴点B横坐标为3，
∴B（3，7）．
故答案为：（3，7）．
点评 题目考查了平面直角坐标系中利用图形求点的坐标，题目整体较为简单，解决题目的关键是利用AB长度和AB线段特殊性求点B坐标．
练习册系列答案
教材全解字词句篇系列答案
相关题目
7．化简（x-1-1）-1的结果是（ ）
| A． | $\frac{x}{1-x}$ | B． | $\frac{x}{x-1}$ | C． | x-1 | D． | 1-x |
8．抛物线y=a1x2+b1x+c1绕点（0，2）旋转180°得到抛物线y=a2x2+b2x+c2，则下面等式成立的是（ ）
| A． | a1-a2=0 | B． | b1+b2=0 | C． | c1+c2=4 | D． | $\frac{{b}_{1}}{{a}_{1}}$=$\frac{{b}_{2}}{{a}_{2}}$ |
12．某工艺品生产厂为了按时完成订单，对员工采取生产奖励活动，奖励办法以下表计算奖励金额，但是一个月后还是不能按时完成，厂家请工程师改进工艺流程，提高了产量．改进工艺前一月生产A、B两种工艺品共413件，改进工艺后的第一个月生产这两种工艺品共510件，其中A和B的生产量分别比改进工艺前一个月增长25%和20%．
（1）在工艺改进前一个月，员工共获得奖励金额多少元？
（2）如果某车间员工想获得5500元奖金，需要生产多少件工艺品；
（3）改进工艺前一个月，生产的A、B两种工艺品分别为多少件？
| 产量（x件） | 每件奖励金额（元） |
| 0＜x≤100 | 10 |
| 100＜x≤300 | 20 |
| x＞300 | 30 |
（2）如果某车间员工想获得5500元奖金，需要生产多少件工艺品；
（3）改进工艺前一个月，生产的A、B两种工艺品分别为多少件？
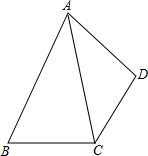如图，AC平分∠BAD，CD=CB，AB＞AD，求证：∠B+∠ADC=180°．
如图，△ABC，△ADE均为等边三角形，AD平分∠BAC交BC于点D，DE交AB于点F．下列结论：①AD⊥BC；②EF=DF；③BE=BD；④BE∥AC．其中正确的有（ ）