题目内容
3.已知二次函数y=x2与一次函数y=2x+3的图象交于A,B两点,求出△AOB的面积.分析 联立两解析式可求得两点的坐标为A(-1,1)、B(3,9),求得直线与y轴的交点C的坐标,然后利用面积和可求得△AOB的面积.
解答 解:联立两函数解析式得$\left\{\begin{array}{l}{y=2x+3}\\{y={x}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=9}\end{array}\right.$,
∴A(-1,1),B(3,9),
设直线y=2x+3与y轴的交点为C,则C(0,3),
∴S△AOB=S△BOC+S△AOC=$\frac{1}{2}$×3×1+$\frac{1}{2}$×3×3=6.
点评 本题主要考查二次函数的性质、一次函数的性质,利用方程组求得交点坐标并把所求三角形的面积转化成两个三角形的面积是解题的关键.

练习册系列答案
相关题目
15.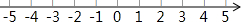 解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
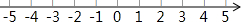 解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
12.一种新病毒的直径约为0.00000043毫米,用科学记数法表示为( )
| A. | 0.43×10-6 | B. | 0.43×106 | C. | 4.3×107 | D. | 4.3×10-7 |
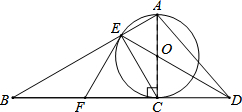 如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.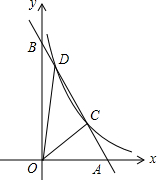 如图,已知直线y1=ax+b与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)两点,连接OC、OD.
如图,已知直线y1=ax+b与x轴、y轴分别交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于C(m,n)、D(p,q)两点,连接OC、OD.