ΧβΡΩΡΎ»ί
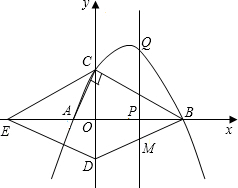 »γΆΦΘ§Ζ÷±π“‘Νβ–ΈBCEDΒΡΕ‘Ϋ«œΏBEΓΔCDΥυ‘Ύ÷±œΏΈΣx÷αΓΔy÷αΫ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§≈ΉΈοœΏy=ax2-6ax-16aΘ®aΘΦ0Θ©ΙΐBΓΔCΝΫΒψΘ§”κx÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψAΘ§«“ΓœACB=90ΓψΘ°ΒψP «x÷α…œ“ΜΕ·ΒψΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®mΘ§0Θ©Θ§ΙΐΒψPΉς÷±œΏl¥Ι÷±”Ύx÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΒψQΘ°
»γΆΦΘ§Ζ÷±π“‘Νβ–ΈBCEDΒΡΕ‘Ϋ«œΏBEΓΔCDΥυ‘Ύ÷±œΏΈΣx÷αΓΔy÷αΫ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§≈ΉΈοœΏy=ax2-6ax-16aΘ®aΘΦ0Θ©ΙΐBΓΔCΝΫΒψΘ§”κx÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψAΘ§«“ΓœACB=90ΓψΘ°ΒψP «x÷α…œ“ΜΕ·ΒψΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®mΘ§0Θ©Θ§ΙΐΒψPΉς÷±œΏl¥Ι÷±”Ύx÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΒψQΘ°Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±ΒψP‘ΎœΏΕΈOB…œ‘ΥΕ· ±Θ§÷±œΏlΫΜBD”ΎΒψMΘ§ ‘ΧΫΨΩΘΚ
ΔΌΧνΩ’ΘΚMQ=
ΔΎΒ±mΈΣΚΈ÷Β ±Θ§ΥΡ±Ώ–ΈCQBMΒΡΟφΜΐ»ΓΒΟΉν¥σ÷ΒΘ§≤Δ«σ≥ω’βΗωΉν¥σ÷ΒΘ°
Θ®3Θ©Β±ΒψP‘ΎœΏΕΈEB…œ‘ΥΕ· ±Θ§ «Ζώ¥φ‘ΎΒψQΘ§ ΙΓςBDQΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψQΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ
Ζ÷ΈωΘΚΘ®1Θ©œ»Α―y=0¥ζ»κy=ax2-6ax-16aΘ§ΒΟΒΫax2-6ax-16a=0Θ§”…aΘΦ0Θ§ΫβΖΫ≥Χx2-6x-16=0«σ≥ωx1=-2Θ§x2=8Θ§ΒΟΒΫAΘ®-2Θ§0Θ©Θ§BΘ®8Θ§0Θ©Θ§‘Ό”…ΓςAOCΓΉΓςCOBΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΕ‘”Π±Ώ≥…±»άΐΒΟ≥ωOC2=OA•OB=16Θ§«σ≥ωOC=4Θ§ΒΟΒΫCΘ®0Θ§4Θ©Θ§»ΜΚσΑ―ΒψCΒψΉχ±ξ¥ζ»κy=ax2-6ax-16aΘ§«σ≥ωa=-
Θ§Φ¥Ω…«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΔΌœ»”…ΒψCΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ§ΒΟ≥ωDΒψΉχ±ξΘ§‘Ό…η÷±œΏBDΒΡΫβΈω ΫΈΣy=kx+bΘ§Α―ΒψBΘ§ΒψDΒΡΉχ±ξ¥ζ»κΘ§‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏBDΒΡΫβΈω ΫΈΣy=
x-4Θ§…ηQΘ®mΘ§-
m2+
m+4ȩȧMȮmȧ
m-4Θ©Θ§‘ρQM=Θ®-
m2+
m+4Θ©-Θ®
m-4Θ©=-
m2+m+8ΘΜ
ΔΎΙΐΒψCΉςCNΓΆQM”ΎNΘ°œ»”…SΥΡ±Ώ–ΈCQBM=SΓςQMC+SΓςQMB=
QM•OBΘ§ΫΪ ΐ÷Β¥ζ»κΒΟΒΫSΥΡ±Ώ–ΈCQBM=-m2+4m+32Θ§‘ΌΗυΨίΕΰ¥ΈΚ· ΐΒΡ–‘÷ Φ¥Ω…«σ≥ωΒ±mΒ»”Ύ2 ±Θ§ΥΡ±Ώ–ΈCQBMΒΡΟφΜΐ»ΓΒΟΉν¥σ÷Β36ΘΜ
Θ®3Θ©Ζ÷»ΐ÷÷«ιΩωΫχ––Χ÷¬έΘΚΔΌΒ±ΓœQBD=90Γψ ±Θ§œ»”…Ά§Ϋ«ΒΡ”ύΫ«œύΒ»ΒΟ≥ωΓœQBP=ΓœBDOΘ§‘ρtanΓœQBP=tanΓœBDOΘ§‘ΌΗυΨί’ΐ«–Κ· ΐΒΡΕ®“εΒΟΒΫΘ®-
m2+
m+4Θ©ΘΚΘ®8-mΘ©=8ΘΚ4Θ§ΫβΖΫ≥Χ«σ≥ωmΒΡ÷ΒΘ§Φ¥Ω…ΒΟΒΫQΒψΒΡΉχ±ξΘΜΔΎΒ±ΓœBDQ=90Γψ ±Θ§œ‘»ΜΒψQ”κΒψA÷ΊΚœΘΜΔέΒ±ΓœBQD=90Γψ ±Θ§ΗυΨί‘≤÷ήΫ«Ε®άμΩ…ΒΟ≤Μ¥φ‘ΎΖϊΚœΧβ“βΒΡΒψQΘ°
| 1 |
| 4 |
Θ®2Θ©ΔΌœ»”…ΒψCΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ§ΒΟ≥ωDΒψΉχ±ξΘ§‘Ό…η÷±œΏBDΒΡΫβΈω ΫΈΣy=kx+bΘ§Α―ΒψBΘ§ΒψDΒΡΉχ±ξ¥ζ»κΘ§‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏBDΒΡΫβΈω ΫΈΣy=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
ΔΎΙΐΒψCΉςCNΓΆQM”ΎNΘ°œ»”…SΥΡ±Ώ–ΈCQBM=SΓςQMC+SΓςQMB=
| 1 |
| 2 |
Θ®3Θ©Ζ÷»ΐ÷÷«ιΩωΫχ––Χ÷¬έΘΚΔΌΒ±ΓœQBD=90Γψ ±Θ§œ»”…Ά§Ϋ«ΒΡ”ύΫ«œύΒ»ΒΟ≥ωΓœQBP=ΓœBDOΘ§‘ρtanΓœQBP=tanΓœBDOΘ§‘ΌΗυΨί’ΐ«–Κ· ΐΒΡΕ®“εΒΟΒΫΘ®-
| 1 |
| 4 |
| 3 |
| 2 |
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©Ννy=0Θ§‘ρax2-6ax-16a=0Θ§
ΓΏaΘΦ0Θ§
Γύx2-6x-16=0Θ§
Γύx1=-2Θ§x2=8Θ§
ΓύAΘ®-2Θ§0Θ©Θ§BΘ®8Θ§0Θ©Θ§
ΓύOA=2Θ§OB=8Θ°
ΓΏΓœACB=90ΓψΘ§OCΓΆABΘ§
ΓύΓςAOCΓΉΓςCOBΘ§
ΓύOC2=OA•OBΘ§
ΓύOC2=2ΓΝ8=16Θ§
”÷OCΘΨ0Θ§
ΓύOC=4Θ§
ΓύCΘ®0Θ§4Θ©Θ°
Α―ΒψCΘ®0Θ§4Θ©¥ζ»κy=ax2-6ax-16aΘ§
ΒΟ-16a=4Θ§ΫβΒΟa=-
Θ§
Γύy=-
x2+
x+4ΘΜ
Θ®2Θ©ΔΌ…η÷±œΏBDΒΡΫβΈω ΫΈΣy=kx+bΘ§
ΓΏΒψCΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ§
ΓύDΘ®0Θ§-4Θ©Θ°
Α―ΒψBΘ§ΒψDΒΡΉχ±ξ¥ζ»κ…œ ΫΘ§
ΒΟ
Θ§ΫβΒΟ
Θ§
 Γύ÷±œΏBDΒΡΫβΈω ΫΈΣy=
Γύ÷±œΏBDΒΡΫβΈω ΫΈΣy=
x-4Θ°
…ηQΘ®mΘ§-
m2+
m+4ȩȧMȮmȧ
m-4Θ©Θ§
ΓύQM=Θ®-
m2+
m+4Θ©-Θ®
m-4Θ©=-
m2+m+8Θ°
Ι ¥πΑΗΈΣ-
m2+m+8ΘΜ
ΔΎ»γΆΦΘ§ΙΐΒψCΉςCNΓΆQM”ΎNΘ°
ΓΏSΥΡ±Ώ–ΈCQBM=SΓςQMC+SΓςQMB=
QM•CN+
QM•PB=
QMΘ®CN+PBΘ©=
QMΘ®OP+PBΘ©=
QM•OBΘ§
ΓύSΥΡ±Ώ–ΈCQBM=
ΓΝΘ®-
m2+m+8Θ©ΓΝ8=-m2+4m+32=-Θ®m-2Θ©2+36Θ§
ΓύΒ±mΒ»”Ύ2 ±Θ§ΥΡ±Ώ–ΈCQBMΒΡΟφΜΐ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ36ΘΜ
 Θ®3Θ©Β±ΒψP‘ΎœΏΕΈEB…œ‘ΥΕ· ±Θ§¥φ‘ΎΒψQΘ®-2Θ§0Θ©ΜρQΘ®6Θ§4Θ©Θ§ ΙΓςBDQΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°άμ”…»γœ¬ΘΚ
Θ®3Θ©Β±ΒψP‘ΎœΏΕΈEB…œ‘ΥΕ· ±Θ§¥φ‘ΎΒψQΘ®-2Θ§0Θ©ΜρQΘ®6Θ§4Θ©Θ§ ΙΓςBDQΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°άμ”…»γœ¬ΘΚ
Ζ÷»ΐ÷÷«ιΩωΘΚ
ΔΌΒ±ΓœQBD=90Γψ ±Θ§»γΆΦΘ°
ΓΏΓœQBP+ΓœPBD=90ΓψΘ§ΓœPBD+ΓœBDO=90ΓψΘ§
ΓύΓœQBP=ΓœBDOΘ§
ΓύtanΓœQBP=tanΓœBDOΘ§
Φ¥Θ®-
m2+
m+4Θ©ΘΚΘ®8-mΘ©=8ΘΚ4Θ§
’ϊάμΘ§ΒΟm2-14m+48=0Θ§
ΫβΒΟm1=6Θ§m2=8Θ®…α»ΞΘ©Θ§
ΓύQΘ®6Θ§4Θ©ΘΜ
ΔΎΒ±ΓœBDQ=90Γψ ±Θ§œ‘»ΜΒψQ”κΒψA÷ΊΚœΘ§
ΓύQΘ®-2Θ§0Θ©ΘΜ
ΔέΒ±ΓœBQD=90Γψ ±Θ§“‘BDΈΣ÷±ΨΕΒΡ‘≤”ΠΗΟΙΐΒψQΘ§ΒΪ «Θ§≤ΜΡ―ΖΔœ÷Θ§“‘BDΈΣ÷±ΨΕΒΡ‘≤Ψ≠ΙΐΒψOΘ§”κ≈ΉΈοœΏΒΡΫΜΒψ «BΘ§Ι ≤Μ¥φ‘ΎΖϊΚœΧβ“βΒΡΒψQΘΜ
Ήέ…œΥυ ωΘ§Υυ«σΒψQΒΡΉχ±ξΈΣΘ®6Θ§4Θ©ΜρΘ®-2Θ§0Θ©Θ°
ΓΏaΘΦ0Θ§
Γύx2-6x-16=0Θ§
Γύx1=-2Θ§x2=8Θ§
ΓύAΘ®-2Θ§0Θ©Θ§BΘ®8Θ§0Θ©Θ§
ΓύOA=2Θ§OB=8Θ°
ΓΏΓœACB=90ΓψΘ§OCΓΆABΘ§
ΓύΓςAOCΓΉΓςCOBΘ§
ΓύOC2=OA•OBΘ§
ΓύOC2=2ΓΝ8=16Θ§
”÷OCΘΨ0Θ§
ΓύOC=4Θ§
ΓύCΘ®0Θ§4Θ©Θ°
Α―ΒψCΘ®0Θ§4Θ©¥ζ»κy=ax2-6ax-16aΘ§
ΒΟ-16a=4Θ§ΫβΒΟa=-
| 1 |
| 4 |
Γύy=-
| 1 |
| 4 |
| 3 |
| 2 |
Θ®2Θ©ΔΌ…η÷±œΏBDΒΡΫβΈω ΫΈΣy=kx+bΘ§
ΓΏΒψCΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ§
ΓύDΘ®0Θ§-4Θ©Θ°
Α―ΒψBΘ§ΒψDΒΡΉχ±ξ¥ζ»κ…œ ΫΘ§
ΒΟ
|
|
 Γύ÷±œΏBDΒΡΫβΈω ΫΈΣy=
Γύ÷±œΏBDΒΡΫβΈω ΫΈΣy=| 1 |
| 2 |
…ηQΘ®mΘ§-
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
ΓύQM=Θ®-
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
Ι ¥πΑΗΈΣ-
| 1 |
| 4 |
ΔΎ»γΆΦΘ§ΙΐΒψCΉςCNΓΆQM”ΎNΘ°
ΓΏSΥΡ±Ώ–ΈCQBM=SΓςQMC+SΓςQMB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
ΓύSΥΡ±Ώ–ΈCQBM=
| 1 |
| 2 |
| 1 |
| 4 |
ΓύΒ±mΒ»”Ύ2 ±Θ§ΥΡ±Ώ–ΈCQBMΒΡΟφΜΐ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ36ΘΜ
 Θ®3Θ©Β±ΒψP‘ΎœΏΕΈEB…œ‘ΥΕ· ±Θ§¥φ‘ΎΒψQΘ®-2Θ§0Θ©ΜρQΘ®6Θ§4Θ©Θ§ ΙΓςBDQΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°άμ”…»γœ¬ΘΚ
Θ®3Θ©Β±ΒψP‘ΎœΏΕΈEB…œ‘ΥΕ· ±Θ§¥φ‘ΎΒψQΘ®-2Θ§0Θ©ΜρQΘ®6Θ§4Θ©Θ§ ΙΓςBDQΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°άμ”…»γœ¬ΘΚΖ÷»ΐ÷÷«ιΩωΘΚ
ΔΌΒ±ΓœQBD=90Γψ ±Θ§»γΆΦΘ°
ΓΏΓœQBP+ΓœPBD=90ΓψΘ§ΓœPBD+ΓœBDO=90ΓψΘ§
ΓύΓœQBP=ΓœBDOΘ§
ΓύtanΓœQBP=tanΓœBDOΘ§
Φ¥Θ®-
| 1 |
| 4 |
| 3 |
| 2 |
’ϊάμΘ§ΒΟm2-14m+48=0Θ§
ΫβΒΟm1=6Θ§m2=8Θ®…α»ΞΘ©Θ§
ΓύQΘ®6Θ§4Θ©ΘΜ
ΔΎΒ±ΓœBDQ=90Γψ ±Θ§œ‘»ΜΒψQ”κΒψA÷ΊΚœΘ§
ΓύQΘ®-2Θ§0Θ©ΘΜ
ΔέΒ±ΓœBQD=90Γψ ±Θ§“‘BDΈΣ÷±ΨΕΒΡ‘≤”ΠΗΟΙΐΒψQΘ§ΒΪ «Θ§≤ΜΡ―ΖΔœ÷Θ§“‘BDΈΣ÷±ΨΕΒΡ‘≤Ψ≠ΙΐΒψOΘ§”κ≈ΉΈοœΏΒΡΫΜΒψ «BΘ§Ι ≤Μ¥φ‘ΎΖϊΚœΧβ“βΒΡΒψQΘΜ
Ήέ…œΥυ ωΘ§Υυ«σΒψQΒΡΉχ±ξΈΣΘ®6Θ§4Θ©ΜρΘ®-2Θ§0Θ©Θ°
ΒψΤάΘΚ±ΨΧβ «Εΰ¥ΈΚ· ΐΒΡΉέΚœΧβ–ΆΘ§Τδ÷–…φΦΑΒΫΒΡ÷Σ ΕΒψ”–‘Υ”Ο¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΓΔ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘ§œύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®”κ–‘÷ Θ§Εΰ¥ΈΚ· ΐΒΡ–‘÷ Θ§ΥΡ±Ώ–ΈΒΡΟφΜΐΘ§÷±Ϋ«»ΐΫ«–ΈΒΡ≈–Ε®Β»÷Σ ΕΘ°‘Υ”ΟΖ÷άύΧ÷¬έΓΔ ΐ–ΈΫαΚœΦΑΖΫ≥ΧΥΦœκ «ΫβΧβΒΡΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
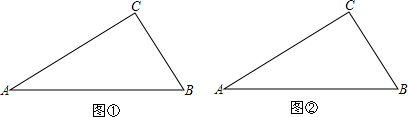
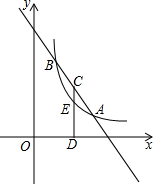 »γΆΦΘ§“Μ¥ΈΚ· ΐy1=-x+4ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐy2=
»γΆΦΘ§“Μ¥ΈΚ· ΐy1=-x+4ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐy2=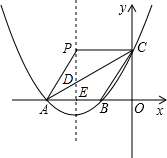 »γΆΦΘ§“―÷Σ≈ΉΈοœΏy=ax2+4ax+tΘ®aΘΨ0Θ©ΫΜx÷α”ΎAΓΔBΝΫΒψΘ§ΫΜy÷α”ΎΒψCΘ§ΒψBΒΡΉχ±ξΈΣΘ®-1Θ§0Θ©Θ°
»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=ax2+4ax+tΘ®aΘΨ0Θ©ΫΜx÷α”ΎAΓΔBΝΫΒψΘ§ΫΜy÷α”ΎΒψCΘ§ΒψBΒΡΉχ±ξΈΣΘ®-1Θ§0Θ©Θ° »γΆΦΘ§’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ4Θ§ΒψE‘Ύ±ΏBC…œΘ§ΥΡ±Ώ–ΈEFGB“≤ «’ΐΖΫ–ΈΘ§“‘BΈΣ‘≤–ΡΘ§BAΒΡ≥ΛΈΣΑκΨΕΜ≠ΜΓACΘ§Ν§Ϋ”AFΘ§CFΘ§«σΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
»γΆΦΘ§’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ4Θ§ΒψE‘Ύ±ΏBC…œΘ§ΥΡ±Ώ–ΈEFGB“≤ «’ΐΖΫ–ΈΘ§“‘BΈΣ‘≤–ΡΘ§BAΒΡ≥ΛΈΣΑκΨΕΜ≠ΜΓACΘ§Ν§Ϋ”AFΘ§CFΘ§«σΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ° »γΆΦΘ§MΈΣΥΪ«ζœΏy=
»γΆΦΘ§MΈΣΥΪ«ζœΏy= »γΆΦ «ΦΉΓΔ““ΝΫ…δΜς‘ΥΕ·‘±ΒΡ10¥Έ…δΜς―ΒΝΖ≥…Φ®Θ®ΜΖ ΐΘ©ΒΡ’έœΏΆ≥ΦΤΆΦΘ§Ιέ≤λΆΦ–ΈΘ§ΦΉΓΔ““’β10¥Έ…δΜς≥…Φ®ΒΡΖΫ≤νSΦΉ2Θ§S““2÷°ΦδΒΡ¥σ–ΓΙΊœΒ «
»γΆΦ «ΦΉΓΔ““ΝΫ…δΜς‘ΥΕ·‘±ΒΡ10¥Έ…δΜς―ΒΝΖ≥…Φ®Θ®ΜΖ ΐΘ©ΒΡ’έœΏΆ≥ΦΤΆΦΘ§Ιέ≤λΆΦ–ΈΘ§ΦΉΓΔ““’β10¥Έ…δΜς≥…Φ®ΒΡΖΫ≤νSΦΉ2Θ§S““2÷°ΦδΒΡ¥σ–ΓΙΊœΒ «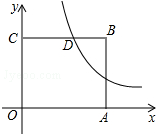 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§’ΐΖΫ–ΈOABCΒΡ±ΏOAΓΔOCΖ÷±π‘Ύx÷αΓΔy÷α…œΘ§ΒψBΒΡΉχ±ξΈΣΘ®4Θ§4Θ©Θ§Ζ¥±»άΐΚ· ΐΒΡΆΦœσΨ≠ΙΐCBΒΡ÷–ΒψDΘ§»τΒψPΘ®xΘ§yΘ©‘ΎΗΟΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œ‘ΥΕ·Θ®≤Μ”κΒψD÷ΊΚœΘ©Θ§ΙΐΒψPΉςPRΓΆy÷α”ΎΒψRΘ§ΉςPQΓΆBCΥυ‘Ύ÷±œΏ”ΎΒψQΘ§Φ«ΥΡ±Ώ–ΈCQPRΒΡΟφΜΐΈΣS=4 ±Θ§xΒΡ÷ΒΈΣ
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§’ΐΖΫ–ΈOABCΒΡ±ΏOAΓΔOCΖ÷±π‘Ύx÷αΓΔy÷α…œΘ§ΒψBΒΡΉχ±ξΈΣΘ®4Θ§4Θ©Θ§Ζ¥±»άΐΚ· ΐΒΡΆΦœσΨ≠ΙΐCBΒΡ÷–ΒψDΘ§»τΒψPΘ®xΘ§yΘ©‘ΎΗΟΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œ‘ΥΕ·Θ®≤Μ”κΒψD÷ΊΚœΘ©Θ§ΙΐΒψPΉςPRΓΆy÷α”ΎΒψRΘ§ΉςPQΓΆBCΥυ‘Ύ÷±œΏ”ΎΒψQΘ§Φ«ΥΡ±Ώ–ΈCQPRΒΡΟφΜΐΈΣS=4 ±Θ§xΒΡ÷ΒΈΣ