题目内容
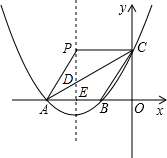 如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).(1)求此抛物线的对称轴及点A的坐标;
(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能判断四边形ABCP是什么四边形吗?请证明你的结论;
(3)连结AC,BP,若AC⊥BP,试求此抛物线的解析式.
考点:二次函数综合题
专题:
分析:(1)直接利用配方法求出抛物线对称轴即可,再利用二次函数对称性得出A点坐标;
(2)首先得出CP=AB,再利用平行四边形的判定方法一组对边平行且相等的四边形是平行四边形得出即可;
(3)利用菱形的判定与性质得出C点坐标,进而利用待定系数法求二次函数解析式.
(2)首先得出CP=AB,再利用平行四边形的判定方法一组对边平行且相等的四边形是平行四边形得出即可;
(3)利用菱形的判定与性质得出C点坐标,进而利用待定系数法求二次函数解析式.
解答: 解:(1)∵y=ax2+4ax+t=a(x+2)2+t-2,
解:(1)∵y=ax2+4ax+t=a(x+2)2+t-2,
∴抛物线的对称轴是直线x=-2,
设点A的坐标为(x,0),
∵
=-2,∴x=-3,
∴A的坐标(-3,0);
(2)四边形ABCP是平行四边形.
理由:
∵抛物线的对称轴是直线x=-2,∴CP=2.
又∵AB=2,∴CP=AB.
又∵CP∥AB,∴四边形ABCP是平行四边形;
(3)∵AC⊥BP,∴平行四边形ABCP是菱形.
∴BC=AB=2.
又∵OB=1,∴OC=
.∴C(0,
).
将B(-1,0),C(0,
)代入y=ax2+4ax+t,得:
,
解得:
,
∴此抛物线的解析式为:y=
x2+
x+
.
 解:(1)∵y=ax2+4ax+t=a(x+2)2+t-2,
解:(1)∵y=ax2+4ax+t=a(x+2)2+t-2,∴抛物线的对称轴是直线x=-2,
设点A的坐标为(x,0),
∵
| -1+x |
| 2 |
∴A的坐标(-3,0);
(2)四边形ABCP是平行四边形.
理由:
∵抛物线的对称轴是直线x=-2,∴CP=2.
又∵AB=2,∴CP=AB.
又∵CP∥AB,∴四边形ABCP是平行四边形;
(3)∵AC⊥BP,∴平行四边形ABCP是菱形.
∴BC=AB=2.
又∵OB=1,∴OC=
| 3 |
| 3 |
将B(-1,0),C(0,
| 3 |
|
解得:
|
∴此抛物线的解析式为:y=
| ||
| 3 |
4
| ||
| 3 |
| 3 |
点评:此题主要考查了待定系数法求二次函数解析式以及平行四边形的判定与性质以及菱形的性质等知识,得出C点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
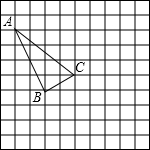 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).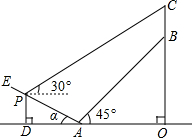 如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=
如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=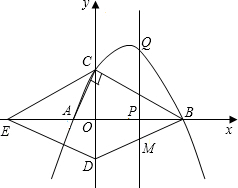 如图,分别以菱形BCED的对角线BE、CD所在直线为x轴、y轴建立平面直角坐标系,抛物线y=ax2-6ax-16a(a<0)过B、C两点,与x轴的负半轴交于点A,且∠ACB=90°.点P是x轴上一动点,设点P的坐标为(m,0),过点P作直线l垂直于x轴,交抛物线于点Q.
如图,分别以菱形BCED的对角线BE、CD所在直线为x轴、y轴建立平面直角坐标系,抛物线y=ax2-6ax-16a(a<0)过B、C两点,与x轴的负半轴交于点A,且∠ACB=90°.点P是x轴上一动点,设点P的坐标为(m,0),过点P作直线l垂直于x轴,交抛物线于点Q.