题目内容
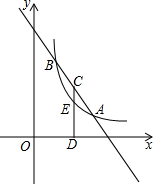 如图,一次函数y1=-x+4的图象与反比例函数y2=
如图,一次函数y1=-x+4的图象与反比例函数y2=| k |
| x |
(1)求反比例函数y2的解析式;
(2)已知点C是AB的中点,过点C作x轴的垂线,垂足为D,CD与反比例函数的图象交于点E,求CE的长.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)点A在直线y1=-x+4上,将A代入得a=1,所以A点的坐标为:(3,1),代入y2=
(x>0)可解得反比例函数y2的解析式.
(2)解
可得B点的坐标为(1,3),根据A、B点的坐标可求得E点的坐标,从而求得CE的值.
| k |
| x |
(2)解
|
解答:解:(1)∵点A在直线y1=-x+4上,将A代入得a=1,
∴A点的坐标为(3,1)代入y2=
(x>0)
解得k=3,
∴解析式为y2=
,
(2)解
得
或
∴B点的坐标为(1,3)
∴C点的纵坐标为2,代入解析式y1=-x+4,
解得 x=2,
将x=2代入y=
,解得y=
∴E点的坐标(2,
),
∴CE=2-
=
∴A点的坐标为(3,1)代入y2=
| k |
| x |
解得k=3,
∴解析式为y2=
| 3 |
| x |
(2)解
|
得
|
|
∴B点的坐标为(1,3)
∴C点的纵坐标为2,代入解析式y1=-x+4,
解得 x=2,
将x=2代入y=
| 3 |
| x |
| 3 |
| 2 |
∴E点的坐标(2,
| 3 |
| 2 |
∴CE=2-
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
-5的相反数是( )
A、
| ||
B、-
| ||
| C、-5 | ||
| D、5 |
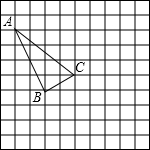 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-2,4),(2,1).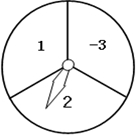 如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).
如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).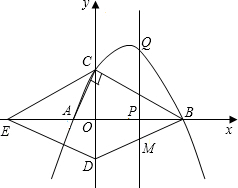 如图,分别以菱形BCED的对角线BE、CD所在直线为x轴、y轴建立平面直角坐标系,抛物线y=ax2-6ax-16a(a<0)过B、C两点,与x轴的负半轴交于点A,且∠ACB=90°.点P是x轴上一动点,设点P的坐标为(m,0),过点P作直线l垂直于x轴,交抛物线于点Q.
如图,分别以菱形BCED的对角线BE、CD所在直线为x轴、y轴建立平面直角坐标系,抛物线y=ax2-6ax-16a(a<0)过B、C两点,与x轴的负半轴交于点A,且∠ACB=90°.点P是x轴上一动点,设点P的坐标为(m,0),过点P作直线l垂直于x轴,交抛物线于点Q.