题目内容
 如图,M为双曲线y=
如图,M为双曲线y=
| ||
| x |
考点:反比例函数综合题
专题:综合题
分析:作CE⊥x轴于E,DF⊥y轴于F,如图所示,根据直线y=-x+m,表示出A与B坐标,可得出三角形OAB为等腰直角三角形,进而确定出三角形ADF与三角形CEB都为等腰直角三角形,设M(a,b),代入反比例解析式得到ab=
,CE=b,DF=a,表示出AD与BC,即可求出AD•BC的值.
| 6 |
解答: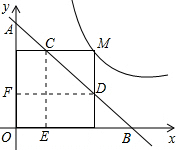 解:作CE⊥x轴于E,DF⊥y轴于F,如图,
解:作CE⊥x轴于E,DF⊥y轴于F,如图,
对于y=-x+m,
令x=0,得到y=m;令y=0,得到x=m,
∴A(0,m),B(m,0),
∴△OAB为等腰直角三角形,
∴△ADF与△CEB都是等腰直角三角形,
设M(a,b),则ab=
,CE=b,DF=a,
∴AD=
DF=
a,BC=
CE=
b,
∴AD•BC=
a•
b=2ab=2
.
故答案为:2
.
 解:作CE⊥x轴于E,DF⊥y轴于F,如图,
解:作CE⊥x轴于E,DF⊥y轴于F,如图,对于y=-x+m,
令x=0,得到y=m;令y=0,得到x=m,
∴A(0,m),B(m,0),
∴△OAB为等腰直角三角形,
∴△ADF与△CEB都是等腰直角三角形,
设M(a,b),则ab=
| 6 |
∴AD=
| 2 |
| 2 |
| 2 |
| 2 |
∴AD•BC=
| 2 |
| 2 |
| 6 |
故答案为:2
| 6 |
点评:此题属于反比例函数综合题,涉及的知识有:等腰直角三角形的性质,坐标与图形性质,反比例函数的性质,以及矩形的性质,熟练掌握等腰直角三角形的性质是解本题的关键.

练习册系列答案
相关题目
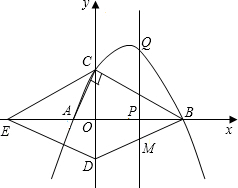 如图,分别以菱形BCED的对角线BE、CD所在直线为x轴、y轴建立平面直角坐标系,抛物线y=ax2-6ax-16a(a<0)过B、C两点,与x轴的负半轴交于点A,且∠ACB=90°.点P是x轴上一动点,设点P的坐标为(m,0),过点P作直线l垂直于x轴,交抛物线于点Q.
如图,分别以菱形BCED的对角线BE、CD所在直线为x轴、y轴建立平面直角坐标系,抛物线y=ax2-6ax-16a(a<0)过B、C两点,与x轴的负半轴交于点A,且∠ACB=90°.点P是x轴上一动点,设点P的坐标为(m,0),过点P作直线l垂直于x轴,交抛物线于点Q.