Question

20．已知⊙O的直径为6，弦AB=3，则弦AB所对的圆周角度数为30°或150°．

Answer 1

分析 先根据题意画出图形，连接OA、OB，过O作OF⊥AB，由垂径可求出AF的长，根据特殊角的三角函数值可求出∠AOF的度数，由圆周角定理及圆内接四边形的性质即可求出答案．

解答 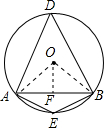解：如图所示，
连接OA、OB，过O作OF⊥AB，则AF=$\frac{1}{2}$AB，∠AOF=$\frac{1}{2}$∠AOB，
∵OA=$\frac{1}{2}×6$=3，AB=3，
∴AF=$\frac{1}{2}$AB=$\frac{1}{2}$×3=$\frac{3}{2}$，
∴sin∠AOF=$\frac{AF}{OA}$=$\frac{1}{2}$，
∴∠AOF=30°，
∴∠AOB=2∠AOF=60°，
∴∠ADB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°，
∴∠AEB=180°-30°=150°．
综上所述：弦AB所对的圆周角度数为30°或150°．
故答案为：30°或150°．

点评 本题考查的是圆周角定理及垂径定理，解答此题时要注意一条弦所对的圆周角有两个，这两个角互为补角．