题目内容
10. 如图,在△ABC中,已知$AB=\sqrt{6}$,∠B=45°,∠C=60°,求△ABC的面积.
如图,在△ABC中,已知$AB=\sqrt{6}$,∠B=45°,∠C=60°,求△ABC的面积.
分析 根据在△ABC中,已知$AB=\sqrt{6}$,∠B=45°,∠C=60°,可以求得BC边上高AD的长和BC的长,从而可以求得△ABC的面积.
解答 解:作BC边上高AD交BC于点D,如下图所示: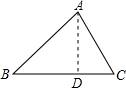
∵在△ABC中,已知$AB=\sqrt{6}$,∠B=45°,sinB=$\frac{AD}{AB}$
∴sin45°=$\frac{AD}{\sqrt{6}}$
解得,AD=$\sqrt{3}$
∴BD=AD=$\sqrt{3}$,
又∵∠C=60°,∠ADC=90°,AD=$\sqrt{3}$,tanC=$\frac{AD}{CD}$,
∴CD=$\frac{AD}{tan60°}=\frac{\sqrt{3}}{\sqrt{3}}=1$,
∴BC=BD+CD=$\sqrt{3}+1$,
∴${S}_{△ABC}=\frac{AD×BC}{2}=\frac{\sqrt{3}×(\sqrt{3}+1)}{2}$=$\frac{3+\sqrt{3}}{2}$,
即△ABC的面积是$\frac{3+\sqrt{3}}{2}$.
点评 本题考查解直角三角形,解题的关键是求出BC上的高AD的长和BC的长.

练习册系列答案
相关题目
1.4的平方根是( )
| A. | 4 | B. | -4 | C. | 2 | D. | ±2 |
19.下列命题中,是真命题的是( )
| A. | 周长相等的等边三角形都全等 | |
| B. | 周长相等的直角三角形都全等 | |
| C. | 如果两个三角形的两边及其中一边的对角对应相等,则这两个三角形全等 | |
| D. | 如果两个三角形的三个角对应相等,则这两个三角形全等 |