题目内容
15.先化简再求值:(1)6x2-(2x-1)(3x-2)+(x+2)(x-2),其中x=3.
(2)先化简:$\frac{2a-4}{{a}^{2}-4}÷\frac{2a}{a+2}+1$,再用一个你最喜欢的数代替计算结果.
分析 (1)先根据整式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=6x2-(6x2-4x-3x+2)+x2-4
=6x2-6x2+4x+3x-2+x2-4
=x2+7x-6.
当x=3时,原式=9+21-6=24;
(2)原式=$\frac{2(a-2)}{(a+2)(a-2)}$•$\frac{a+2}{2a}$+1
=$\frac{1}{a}$+1.
当a=1时,原式=1+1=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
5.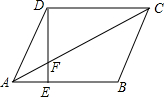 如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
 如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )| A. | 12cm2 | B. | 24cm2 | C. | 36cm2 | D. | 48cm2 |