题目内容
2.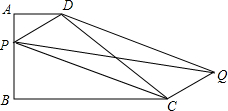 已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.问题1:如图,P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
分析 四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形,然后利用矩形的性质,设PB=x,可得方程x2+32+(2-x)2+1=(2$\sqrt{2}$)2,由判别式△<0,可知此方程无实数根,即对角线PQ,DC的长不可能相等.
解答 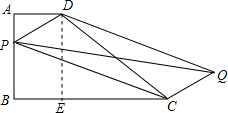 解:对角线PQ与DC不能相等,理由如下:
解:对角线PQ与DC不能相等,理由如下:
过点D作DE⊥BC于点E,
∵梯形ABCD,AD∥BC,AB⊥BC,
∴四边形ABED是矩形,
∴DE=AB=2,BE=AD=1,
∴CE=BC-BE=2,
∴DC=2$\sqrt{2}$,
∵四边形PCQD是平行四边形,
若对角线PQ、DC相等,则四边形PCQD是矩形,
设PB=x,则AP=2-x,
在Rt△DPC中,PD2+PC2=DC2,即x2+32+(2-x)2+1=(2$\sqrt{2}$)2,
化简得x2-2x+3=0,
∵△=(-2)2-4×1×3=-8<0,
∴此方程无实数根,
∴即对角线PQ与DC不能相等.
点评 此题考查了平行四边形的性质、矩形的判定与性质、勾股定理,注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
 如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )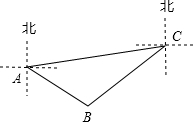 如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,A,B,C分别表示三个小岛上的点,点C在点A的北偏东80°方向,点B在点A的南偏东55°方向,且A,B两点的距离约为6km;同时点B在点C的南偏西50°方向.求A,C两点之间的距离.(结果精确到0.01km.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)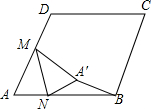 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′B,请求出A′B长度的最小值.
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′B,请求出A′B长度的最小值.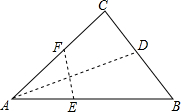 如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AC=10cm,AB=15cm,按下列步骤折叠:第一次,过点A折叠,使C点落在AB边上,折痕交BC边于D点;第二次折叠,使点A与点D重合,折痕分别交AB、AC边于点E、F,展开后,连结DE、DF.