题目内容
7.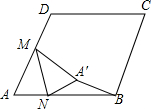 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′B,请求出A′B长度的最小值.
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′B,请求出A′B长度的最小值.
分析 利用已知点A′在以AD为直径的圆上,得出当点A′在BM上时,A′B长度取得最小值,进而得出BM的长,即可得出答案;
解答  解:如图,由折叠知A′M=AM,又M是AD的中点,可得MA=MA′=MD,
解:如图,由折叠知A′M=AM,又M是AD的中点,可得MA=MA′=MD,
故点A′在以AD为直径的圆上,
由模型可知,当点A′在BM上时,A′B长度取得最小值,
∵边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,
∴BM=$\sqrt{{2}^{2}-1}$=$\sqrt{3}$,
故A′B的最小值为:$\sqrt{3}$-1.
点评 此题主要考查了菱形的性质以及勾股定理,得出A′点位置是解题关键.

练习册系列答案
相关题目
4.下列各点,在抛物线y=(x-2)2+2上的点是( )
| A. | (0,4) | B. | (2,0) | C. | (2,2) | D. | (0,-2) |
 在△ABC中,AB=10cm,AC=8cm,边BC的垂直平分线分别交AB,BC于点E,D,求△ACE的周长.
在△ABC中,AB=10cm,AC=8cm,边BC的垂直平分线分别交AB,BC于点E,D,求△ACE的周长.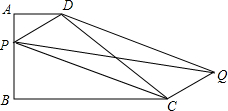 已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.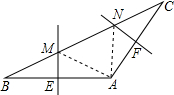 在△ABC中,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.
在△ABC中,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F.