题目内容
13.先化简,再求值:$\frac{x}{{{x^2}-1}}÷(1-\frac{1}{x+1})$,其中x=$\sqrt{3}$+1.分析 根据分式混合运算的法则先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{x}{(x+1)(x-1)}$÷$\frac{x}{x+1}$
=$\frac{x}{(x+1)(x-1)}$•$\frac{x+1}{x}$
=$\frac{1}{x-1}$,
当x=$\sqrt{3}$+1时,原式=$\frac{{\sqrt{3}}}{3}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如图“慢行通过,注意危险,禁止行人通行,禁止非机动车通行”四个交通标志图(黑白阴影图片)中是轴对称图形的是( )
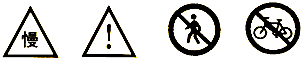
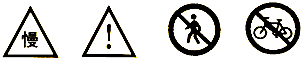
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.若式子$\sqrt{x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≥1 | D. | x≤1 |
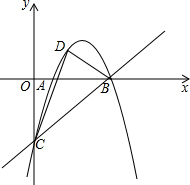 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
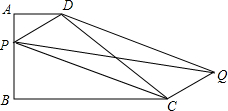 已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.