题目内容
已知a+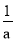 =5,则a2+
=5,则a2+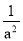 的结果是___________.
的结果是___________.
 23
【解析】由题意知=25,即a2++2=25,所以a2+=23.
23
【解析】由题意知=25,即a2++2=25,所以a2+=23.
练习册系列答案
相关题目
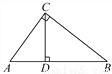
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=4,BC=6,则tan∠ACD的值为( )
A. 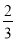 B.
B. 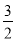 C.
C. 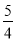 D.
D. 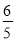
 A
【解析】∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ADC=90°,∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵tanB =,
∴tan∠ACD =,
故选A.
A
【解析】∵∠ACB=90°,∴∠A+∠B=90°,
∵∠ADC=90°,∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∵tanB =,
∴tan∠ACD =,
故选A. 如图,已知AB∥CD,∠1=100°,∠2=120°,则∠α=_____.
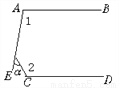
 40°
【解析】
延长AE、DC相交于点F.
∵AB∥CD,∠1=100°,
∴∠F=180°-100°=80°,
∴∠α=∠2-∠F=120°-80°=40°.
40°
【解析】
延长AE、DC相交于点F.
∵AB∥CD,∠1=100°,
∴∠F=180°-100°=80°,
∴∠α=∠2-∠F=120°-80°=40°. 如图,△ABC和△A′B′C′关于直线l对称,下列结论中:
①△ABC≌△A′B′C′;
②∠BAC′=∠B′AC;
③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
正确的有( )
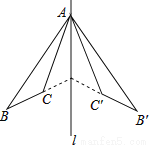
A. 4个 B. 3个 C. 2个 D. 1个
 B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故...
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故... 已知(x2+px+8)(x2-3x+q)的展开式中不含x2和x3项,求p,q的值.
 p=3,q=1.
【解析】试题分析:根据整式的乘法,化简完成后,根据不含项的系数为0求解即可.
试题解析:∵(x2+px+8)(x2﹣3x+q)
=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q
=x4+(p﹣3)x3+(q﹣3p+8)x2+(pq﹣24)x+8q.
∵乘积中不含x2与x3项,
∴p﹣3=0,q﹣3p+8=0,
∴p=...
p=3,q=1.
【解析】试题分析:根据整式的乘法,化简完成后,根据不含项的系数为0求解即可.
试题解析:∵(x2+px+8)(x2﹣3x+q)
=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q
=x4+(p﹣3)x3+(q﹣3p+8)x2+(pq﹣24)x+8q.
∵乘积中不含x2与x3项,
∴p﹣3=0,q﹣3p+8=0,
∴p=... 计算:(-2)2 016+(-2)2 017=___________.
 -22 016
【解析】 (-2)2 016+(-2)2 017=(-2)2 016(1-2)=-22 016.
-22 016
【解析】 (-2)2 016+(-2)2 017=(-2)2 016(1-2)=-22 016. 如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为 ( )
A. –3 B. 3 C. 0 D. 1
 A
【解析】(x+m)(x+3)=x2+(3+m)x+3m,
因为结果不含x的一次项,所以3+m=0,m=-3,
故选A.
A
【解析】(x+m)(x+3)=x2+(3+m)x+3m,
因为结果不含x的一次项,所以3+m=0,m=-3,
故选A. 观察图中的汽车商标,其中是轴对称图形的个数为

A、2 B、3 C、4 D、5
 B
【解析】
试题分析:轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
由图可得轴对称图形为第一个、第二个、第四个,故选B.
B
【解析】
试题分析:轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
由图可得轴对称图形为第一个、第二个、第四个,故选B. 河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有______ 米3的水,水泵最多抽________ 小时,水泵抽8小时后,河道剩水量是________ 米3 .
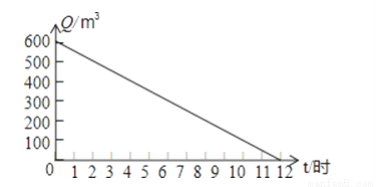
 600 12 200
【解析】观察图象可知, 水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是600-600÷12×8=200米3.
600 12 200
【解析】观察图象可知, 水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是600-600÷12×8=200米3. 
