题目内容
5.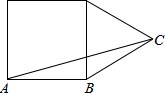 边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为$\frac{1}{4}$.
边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为$\frac{1}{4}$.
分析 过点C作CD和CE垂直正方形的两个边长,再利用正方形和等边三角形的性质得出CE的长,进而得出△ABC的面积即可.
解答 解:过点C作CD和CE垂直正方形的两个边长,如图
∵一个正方形和一个等边三角形的摆放,
∴四边形DBEC是矩形,
∴CE=DB=$\frac{1}{2}$,
∴△ABC的面积=$\frac{1}{2}$AB•CE=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 此题考查正方形的性质,关键是根据正方形和等边三角形的性质得出BE和CE的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.三角形两边长分别为3和6,第三边的长是方程x2-13x+36=0的两根,则该三角形的周长为( )
| A. | 13 | B. | 15 | C. | 18 | D. | 13或18 |
14.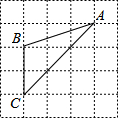 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |

 已知:如图,直线AB与直线DE相交于点C,CF⊥DE,∠ACD=25°,求∠BCE和∠BCF的度数.
已知:如图,直线AB与直线DE相交于点C,CF⊥DE,∠ACD=25°,求∠BCE和∠BCF的度数.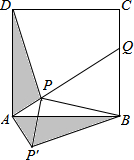 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.