题目内容
13.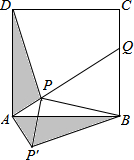 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.
分析 (1)根据旋转的性质可知,△APD≌△AP′B,所以AP=AP′,∠PAD=∠P′AB,因为∠PAD+∠PAB=90°,所以∠P′AB+∠PAB=90°,即∠PAP′=90°,故△APP′是等腰直角三角形;
(2)根据勾股定理逆定理可判断△PP′B是直角三角形,再根据平角定义求出结果;
(3)作BE⊥AQ,垂足为E,由∠BPQ=45°,P′B=2$\sqrt{2}$,求出PE=BE=2,在Rt△ABE中,运用勾股定理求出AB,再由cos∠EAB=cos∠EBQ,求出BQ,则CQ=BC-BQ.
解答 解:(1)∵△ADP沿点A旋转至△ABP′,
∴根据旋转的性质可知,△APD≌△AP′B,
∴AP=AP′,∠PAD=∠P′AB,
∵∠PAD+∠PAB=90°,
∴∠P′AB+∠PAB=90°,
即∠PAP′=90°,
∴△APP′是等腰直角三角形;
(2)由(1)知∠PAP′=90°,AP=AP′=1,
∴PP′=$\sqrt{2}$,
∵P′B=PD=$\sqrt{10}$,PB=2$\sqrt{2}$,
∴P′B2=PP′2+PB2,
∴∠P′PB=90°,
∵△APP′是等腰直角三角形,
∴∠APP′=45°,
∴∠BPQ=180°-90°-45°=45°;
(3)作BE⊥AQ,垂足为E,
∵∠BPQ=45°,PB=2$\sqrt{2}$,
∴PE=BE=2,
∴AE=2+1=3,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{13}$,BE=$\sqrt{13-9}$=2,
∵∠EBQ=∠EAB,cos∠EAB=$\frac{AE}{AB}=\frac{3}{\sqrt{13}}$,
∴cos∠EBQ=$\frac{BE}{BQ}=\frac{3}{\sqrt{13}}$,
∴$\frac{2}{BQ}=\frac{3}{\sqrt{13}}$,
∴BQ=$\frac{2\sqrt{13}}{3}$,
∴CQ=$\sqrt{13}$-$\frac{2\sqrt{13}}{3}$=$\frac{\sqrt{13}}{3}$.
点评 本题主要考查了旋转的性质、全等三角形的判定与性质、勾股定理及逆定理、锐角三角函数的综合运用,有一定难度,作BE⊥AQ,构造等角的余弦值相等列方程或运用相似三角形对应线段成比例求出BQ是解决问题的关键.

| A. | a2<b2 | B. | -3+a<-3+b | C. | -2a>-2b | D. | a3<b3 |
| A. | 3a3b-a2b=2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-1 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 |
 如图,在?ABCD中,对角线AC、BD相交于点O,点E是AB的中点,且OE=3,则AD=6.
如图,在?ABCD中,对角线AC、BD相交于点O,点E是AB的中点,且OE=3,则AD=6. 如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90-$\frac{α}{2}$度(用关于α的代数式表示).
如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90-$\frac{α}{2}$度(用关于α的代数式表示). 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).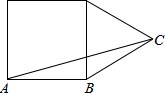 边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为$\frac{1}{4}$.
边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为$\frac{1}{4}$.