题目内容
10.已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2.(1)当P为线段AB的中点时,求d1+d2的值;
(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.
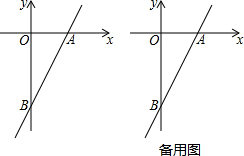
分析 (1)对于一次函数解析式,求出A与B的坐标,即可求出P为线段AB的中点时d1+d2的值;
(2)根据题意确定出d1+d2的范围,设P(m,2m-4),表示出d1+d2,分类讨论m的范围,根据d1+d2=3求出m的值,即可确定出P的坐标;
(3)设P(m,2m-4),表示出d1与d2,由P在线段上求出m的范围,利用绝对值的代数意义表示出d1与d2,代入d1+ad2=4,根据存在无数个点P求出a的值即可.
解答 解:(1)对于一次函数y=2x-4,
令x=0,得到y=-4;令y=0,得到x=2,
∴A(2,0),B(0,-4),
∵P为AB的中点,
∴P(1,-2),
则d1+d2=3;
(2)①d1+d2≥2;
②设P(m,2m-4),
∴d1+d2=|m|+|2m-4|,
当0≤m≤2时,d1+d2=m+4-2m=4-m=3,
解得:m=1,此时P1(1,-2);
当m>2时,d1+d2=m+2m-4=3,
解得:m=$\frac{7}{3}$,此时P2($\frac{7}{3}$,$\frac{2}{3}$);
当m<0时,不存在,
综上,P的坐标为(1,-2)或($\frac{7}{3}$,$\frac{2}{3}$);
(3)设P(m,2m-4),
∴d1=|2m-4|,d2=|m|,
∵P在线段AB上,
∴0≤m≤2,
∴d1=4-2m,d2=m,
∵d1+ad2=4,
∴4-2m+am=4,即(a-2)m=0,
∵有无数个点,
∴a=2.
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,线段中点坐标公式,绝对值的代数意义,以及坐标与图形性质,熟练掌握绝对值的代数意义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列命题正确的是( )
| A. | 一组对边相等,另一组对边平行的四边形是平行四边形 | |
| B. | 对角线相互垂直的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线相互垂直平分且相等的四边形是正方形 |
20. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )| A. | 48° | B. | 36° | C. | 30° | D. | 24° |
 如图,已知四边形ABCD中,∠B=∠D=90°,∠BAD的平分线AE交CD于E,∠DCB的平分线CF交AB于F,试判断AE与CF的位置关系,并说明理由.
如图,已知四边形ABCD中,∠B=∠D=90°,∠BAD的平分线AE交CD于E,∠DCB的平分线CF交AB于F,试判断AE与CF的位置关系,并说明理由. 如图,在?ABCD中,对角线AC、BD相交于点O,点E是AB的中点,且OE=3,则AD=6.
如图,在?ABCD中,对角线AC、BD相交于点O,点E是AB的中点,且OE=3,则AD=6. 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).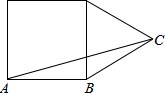 边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为$\frac{1}{4}$.
边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为$\frac{1}{4}$.
