题目内容
16. 如图所示,在△ABC中,AE是BC边上的中线,AD⊥BC于D,且∠1=∠2=∠3,BC=6cm,求AB的长.
如图所示,在△ABC中,AE是BC边上的中线,AD⊥BC于D,且∠1=∠2=∠3,BC=6cm,求AB的长.
分析 由AE是BC边上的中线,得到BE=CE=$\frac{1}{2}$BC,求出BE与CE的长,根据等腰三角形三线合一的性质可得BD=DE=$\frac{1}{2}$BE,求出DE的长,根据角平分线的性质可得DE=EF,求出EF的长,在直角三角形EFC中,根据含30°的直角三角形的性质可得∠C=30°,进一步得到∠BAC=90°,在直角三角形ABC中,根据含30°的直角三角形的性质可得AB的长.
解答 解:∵AE是BC边上的中线,
∴BE=CE=$\frac{1}{2}$BC=3cm,
∵AD⊥BC,∠1=∠2,
∴BD=DE=$\frac{1}{2}$BE=1.5cm,
∵∠2=∠3,
∴DE=EF=1.5cm,
∴在直角三角形EFC中,∠C=30°,
∴∠2=∠3=60°,
∴∠BAC=90°,
∴在直角三角形ABC中,AB=$\frac{1}{2}$BC=3cm.
故AB的长是3cm.
点评 此题考查了等腰三角形三线合一的性质,角平分线的性质,含30°的直角三角形的性质,求得∠C=30°和∠BAC=90°是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.下列说法中,正确的个数为( )
①对于任何有理数m,都有m2>0;
②对于任何有理数m,都有m2=(-m)2;
③对于任何有理数m,n(m≠n),都有(m-n)2>0;
④对于任何有理数m,都有m3=(-m)3.
①对于任何有理数m,都有m2>0;
②对于任何有理数m,都有m2=(-m)2;
③对于任何有理数m,n(m≠n),都有(m-n)2>0;
④对于任何有理数m,都有m3=(-m)3.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
8.若1<x<2,则$\sqrt{{(x-3)}^{2}}$+$\sqrt{{(x-1)}^{2}}$的值为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
 已知AD是BC边上的中线,AF=2FD,求证:AE=EC.
已知AD是BC边上的中线,AF=2FD,求证:AE=EC.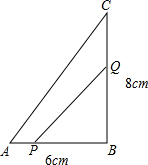 如图,在△ABC中,∠B=90°,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B沿边BC向点C以2cm/s的速度移动.如果点P、Q分别从A、B同时出发.问:
如图,在△ABC中,∠B=90°,点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B沿边BC向点C以2cm/s的速度移动.如果点P、Q分别从A、B同时出发.问: