题目内容
6.用适当的方法解下列方程:(1)3x2-1=6x;
(2)(3x-2)2=(2x-3)2;
(3)y2-2y-399=0;
(4)(3x-2)2-5(3x-2)+4=0.
分析 (1)先移项,再求出b2-4ac的值,最后代入公式求出即可;
(2)移项变形后分解因式得到(5x-5)(x+1)=0,推出方程5x-5=0或x+1=0,求出方程的解即可.
(3)移项后配方得到(y-1)2=400,推出方程y-1=±20,求出方程的解即可;
(4)分解因式得到(3x-3)(3x-6)=0,推出方程3x-3=0或3x-6=0,求出方程的解即可.
解答 解:(1)3x2-1=6x
移项得,3x2-6x-1=0
∵a=3,b=-6,c=-1,
∵b-4ac=36+12=48>0,
∴x=$\frac{6±\sqrt{48}}{2×3}$=$\frac{6±4\sqrt{3}}{6}$
∴x1=$\frac{3+2\sqrt{3}}{3}$,x2=$\frac{3-2\sqrt{3}}{3}$;
(2)(3x-2)2=(2x-3)2
移项变形得:(3x-2)2-(2x-3)2=0,
分解因式得:(3x-2+2x-3)(3x-2-2x+3)=0,
可得5x-5=0或x+1=0,
解得:x1=1,x2=-1;
(3)y2-2y-399=0
移项得:y2-2y=399,
配方得:y2-2y+1=399+1,
即(y-1)2=400,
∴y-1=±20,
∴y1=21,y2=-19;
(4)(3x-2)2-5(3x-2)+4=0
分解因式得:(3x-2-1)(3x-2-4)=0,
可得3x-3=0或3x-6=0,
解得:x1=1,x2=2.
点评 本题考查了解一元二次方程的方法,当把方程通过移项把等式的右边化为0后方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.当化简后不能用分解因式的方法即可考虑配方法和求根公式法.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案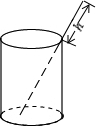 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )| A. | h≤17 | B. | 7≤h≤16 | C. | 15≤h≤16 | D. | h≥8 |
 如图所示,在△ABC中,AE是BC边上的中线,AD⊥BC于D,且∠1=∠2=∠3,BC=6cm,求AB的长.
如图所示,在△ABC中,AE是BC边上的中线,AD⊥BC于D,且∠1=∠2=∠3,BC=6cm,求AB的长.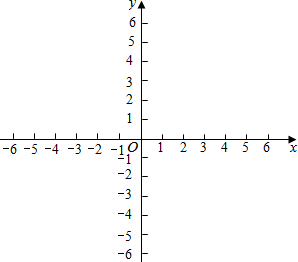 已知:一次函数y=2x-4
已知:一次函数y=2x-4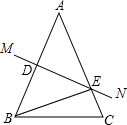 在△ABC中,AB=AC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EBC的周长为25cm,则BC长为11cm.
在△ABC中,AB=AC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EBC的周长为25cm,则BC长为11cm.