题目内容
12.已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
分析 (1)①根据矩形的周长公式即可得到结论;
②根据题意即可得到结论;
(2)根据表中的数据画出函数的图象即可;
(3)结合表中的数据就可以写出图象的相应的性质.
解答  解:(1)①y与x的函数表达式为 y=2x+$\frac{2}{x}$;
解:(1)①y与x的函数表达式为 y=2x+$\frac{2}{x}$;
②自变量x的取值范围是x>0;
故答案为:y=2x+$\frac{2}{x}$,x>0;
(2)①把x=2,y=m代入y=2x+$\frac{2}{x}$,
解得:m=5;
②函数图象如图所示;
③当0<x<1时,y随x增大而减小;当x>1时,y随x增大而增大;当x=1时函数y=2x+$\frac{2}{x}$(x>0)的最小值为2.
点评 本题考查了描点法画函数的图象的方法,二次函数最值的运用.反比例函数的图象性质的运用.

练习册系列答案
相关题目
3.单项式-2a的次数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
7.若3xm+5y2与x3yn的和是单项式,则mn=( )
| A. | 2 | B. | 4 | C. | 8 | D. | 9 |
5.若两个相似三角形的相似比是1:5,那么它们的周长之比是( )
| A. | 1:$\sqrt{5}$ | B. | 1:5 | C. | 1:10 | D. | 1:25 |
 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.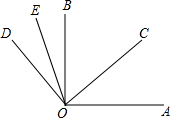 如图,已知∠AOB=90°,∠COE=70°,若OC平分∠AOB,OE平分∠DOB,求:
如图,已知∠AOB=90°,∠COE=70°,若OC平分∠AOB,OE平分∠DOB,求: 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )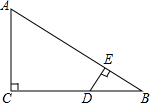 已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.
已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.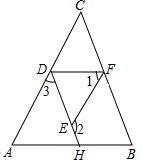 完成推理填空:
完成推理填空: